Линейная зависимость и независимость функций

Функции у₁(х)иу₂(х) называются линейно независимыми на отрезке [a, b], если тождество

С₁ у₁(х) + С₂ у₂(х) º 0, хÎ[a, b], (3)

имеет место тогда и только тогда, когда С₁ = С₂ = 0.

Если же существуют такие числа С₁и С₂ , из которых хотя бы одно отлично от нуля, что для всех хÎ[a, b] имеет место тождество (3), то функции у₁(х)иу₂(х) называются линейно зависимыми на отрезке [a, b].

Данные определения равносильны следующим: функции у₁(х) и у₂(х) называются линейно независимыми (зависимыми)на отрезке [a, b], если у₁(х) ¹ lу₂(х) (у₁(х) = lу₂(х)), хÎ[a, b],

l - const. Другими словами,функции у₁(х) и у₂(х) называются линейно независимыми (зависимыми)на отрезке [a, b], если у₁(х) и у₂(х) непропорциональны (пропорциональны) на отрезке [a, b].

Пример 1. Функции у₁(х) = 3е^х и у₂(х) = е^х линейно зависимы: 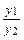= = 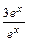3 = const; функции у₁(х) = 3е^х

и у₃(х) = е^2x линейно независимы: 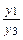= = 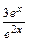3е^–х ≠ const; функции у₄(х) = sin x и у₅(х) = cos x

линейно независимы: равенство С₁sin x + С₂ cos x = 0 выполняется для всех х 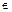R лишь при С₁ = С₂= 0

( или 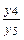= = 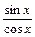tg x ≠ const ).

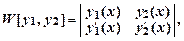О линейной зависимости или независимости функций у₁(х) и у₂(х) можно судить по определителю

который называется определителем Вронского (или просто вронскианом).