МЕТОД ЛАГРАНЖА (МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНОЙ ПОСТОЯННОЙ)

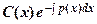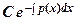Уравнение (1) также можно решить методом вариации произвольной постоянной (метод Лагранжа); в этом случае его общее решение ищется в виде , где – общее решение соответствующего однородного уравнения, где С – const. Т.е. вначале ищется общее решение соответствующего линейного однородного уравнения (2) 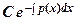, а затем const С заменяется неизвестной функцией С(х).

Пример 12. Проинтегрировать методом Лагранжа уравнение из примера 11: у′ +2ху =2x.

1) Решаем соответствующее однородное уравнение у′ +2ху =0. Это уравнение с разделяющимися переменными 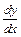= –2хy => 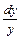= –2хdx => ln |y|= –х² + ln |C|=> y = C .

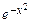2) Заменяем в полученном решении С на С(х), и решение исходного уравнения ищем в виде y = C(х) .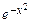

Имеем: у′ = C′(х) 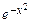– 2х ∙ C(х) 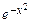. Тогда C′(х) 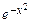– 2х ∙ C(х) 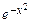+2х C(х) 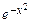=2x или C′(х) 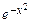= 2х. Это диф.уравнение относительно С(х) с разделяющимися переменными. Решим его: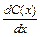 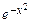=2х =>

dС(х)=2х 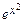dx => С(х)= 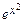+ C. Поэтому y = C(х) 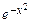= ( 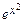+ C) 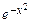= 1 + С .

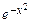Замечание. Уравнение вида (x ∙ P(y) + Q(y)) ∙ y′ = R(y)можно свести к линейному, если

считать х функцией, а у – аргументом: х = х(у). Тогда, пользуясь равенством

у′ = 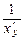, получаем (x ∙ P(y) + Q(y)) / x′_y = R(y), т.е. x′ – x ∙ P(y) / R(y) = Q(y) / R(y) –

линейное относительно х уравнение.

Пример 13. Найти общее решение уравнения (х + у) у′ =1.

Т.к. у′ = 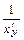, то исходное уравнение имеет вид х′ = х + у – это линейное относительно х(у) уравнение.

Решаем его методом « u на v» : x = uv => x′ = u′v + uv′ и исходное уравнение преобразуется к виду

u′v + uv′ = uv +y или u′v + u (v′ – v)= y.

1) Решим диф.уравнение v′ – v = 0. Имеем 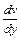= v => 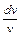= dу => ln |v|= у => v = е^у.

2) Решаем уравнение u′v = у, т.е. u′ е^у = у или u′ = у е^–у => u = 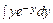. Интегрируя по частям, находим u = –у е^–у – е^–у + С.

3) Общее решение диф.уравнения x = uv = (С – у е^–у – е^–у ) ∙ е^у или x = Се^у – у – 1.

Уравнение вида у¢ + р(х) у = q(x) yⁿ, (3)

где n Î R,n ¹ 0, n ¹ 1, а р(х) и q(x) – непрерывные функции (в частности – постоянные), называется уравнением Бернулли.

Оно приводится к линейному уравнению с помощью подстановки z = y ^–n+1:

=> z′ = 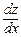= (1 – n) ∙ y ^–n ∙ y′ => y ^–n ∙ y′ = .

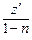Следовательно, уравнение (3) принимает вид 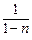z′ + p(x) z = q(x). Это уравнение – линейное относительно z.

На практике уравнение Бернулли, не сводя к линейному, интегрируют с помощью подстановки y = uv (методом Бернулли) или с помощью метода вариации произвольной постоянной (метода Лагранжа).