Уравнения с разделяющимися переменными (УРП)
Дифференциальные уравнения первого порядка
Основные понятия.
Уравнения, связывающие независимую переменную, искомую функцию и ее производные, называются дифференциальными. Если искомая функция зависит от одной переменной, то диф.уравнение называют обыкновенным, в противном случае – в частных производных.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение у′′′ –3у′′ + 2у =0– обыкновенное диф.уравнение 3-го порядка,
уравнение х100у′ + 5ху = у25 – обыкновенное диф.уравнение 1-го порядка,
уравнение y ∙ z′x = x ∙ z′y – диф.уравнение в частных производных 1-го порядка.
Записи ДУ1: F (x, y, y¢) = 0– общий вид, ( 1 )
y¢ = f (x, y)– ДУ, разрешенное относительно производной,
dy = f (x, y) dxили P(x, y) dx + Q(x, y) dy = 0 – дифференциальная форма.
Решением ДУ1 называется любая функция у = j (х), которая при подстановке в это уравнение обращает его в тождество.
График функции у = j (х) называется интегральной кривой.
Процесс нахождения решений данного ДУ называется интегрированием этого уравнения.
Интегрирование ДУ в общем случае приводит к бесконечному множеству решений, отличающихся друг от друга на постоянные величины. Например, очевидно, что решением уравнения
у′ =2х являются функции у = х2, у = х2+ 5, у = х2– 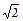 и, вообще, у = х2+ С, где С – const.
и, вообще, у = х2+ С, где С – const.
Геометрически общее решение (общий интеграл) представляет собой семейство интегральных кривых на плоскости Оху.
Среди множества решений можно выбрать одно, задав т.н. начальное условие (НУ)
у(х0) = у0 или y|x = x0 = y0.
Задача отыскания решения ДУ(1), удовлетворяющего заданному нач.условию у(х0) = у0, называется задачей Коши.Геометрически это равносильно следующему: требуется найти интегральную кривую уравнения (1), проходящую через точку М(х0, у0).
Общим решением уравнения (1) называется такая функция у = j (х, С), ( 2 )
где С – произвольная постоянная (const), что:
1) при любом конкретном значении С она является решением этого уравнения;
2) для любого допустимого нач.условия у(х0) = у0 найдется такое значение С = С0,
что j (х0, С0) = у0.
В некоторых случаях общее решение ДУ записывают в неявном виде Ф (х, у, С) = 0. Тогда соотношение Ф (х, у, С) = 0 называется общим интегралом этого уравнения.
Частным решением уравнения (1) называется функция у = j (х, С0), получаемая из общего решения (2) при конкретном значении постоянной С = С0.
Частным интегралом уравнения (1) называется равенство Ф (х, у, С0) = 0, полученное из общего интеграла при фиксированном значении С = С0.
| Теорема1 (Коши) – существования и единственности решения. Пусть в ДУ1 y¢ = f (x, y) функция f (x, y) и ее частная производная f ′¢у (x, y) непрерывны в некоторой области D плоскости Оху. Тогда для любой точки М(х0, у0) Î D существует и притом единственное решение у = у(х) этого уравнения, удовлетворяющее начальному условию у(х0) = у0. |
Геометрический смысл теоремы в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку (х0, у0).
В каждой точке (х0, у0)ÎD число f (х0, у0) выражает угловой коэффициент касательной к кривой у = у(х). Поэтому каждой точке области D уравнение y¢ = f (x, y) ставит в соответствие некоторое направление – геометрически его можно изобразить черточкой (стрелкой), проходящей через эту точку. Тем самым уравнение y¢ = f (x, y), (х, у)ÎD, определяет поле направлений на плоскости.
Множество точек (х, у)ÎD, в которых y¢ = k, где k – const, или, что то же самое, f (x, y) = k (линии уровня функции f (x, y)), называется изоклиной диф.уравнения. В точках изоклины направление поля одинаково, т.е. направления касательных в точках изоклины (или соответствующие черточки) параллельны.
Придавая k близкие числовые значения, можно построить достаточно густую сеть изоклин, а с их помощью – приближенно нарисовать вид интегральных кривых, т.е. решений ДУ. Этот метод, метод изоклин (графический, геометрический) особенно ценен в том случае, когда решение уравнения, общее или частное, не выражается в элементарных функциях – интеграл не берется.















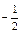
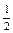
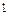 Уравнение изоклины получается, если положить y¢ = с, т.е., f (x, y) = с.
Уравнение изоклины получается, если положить y¢ = с, т.е., f (x, y) = с.
Пример 1. С помощью изоклин начертить вид интегральных кривых уравнения y¢ = 2х.
Уравнения изоклин этого ДУ будет 2х = с, т.е. изоклинами здесь будут прямые,
параллельные оси Оу ( х = 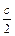 ). В точках этих прямых проведем отрезки, образующие
). В точках этих прямых проведем отрезки, образующие
с осью Ох один и тот же угол α, тангенс которого равен с. Так, при с = 0 имеем
х = 0, tg α = 0 => α = 0; при с = 1 имеем х = 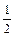 , tg α = 1 => α = 45º;
, tg α = 1 => α = 45º;
при с = –1: х = – 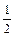 , tg α = –1 => α = –45º; при с = 2 имеем х = 1, tg α = 2 =>
, tg α = –1 => α = –45º; при с = 2 имеем х = 1, tg α = 2 =>
=> α = arctg2 ≈ 63º и т.д. Построив четыре изоклины и отметив на них ряд стрелочек, Рис.1.
наклоненных к оси Ох под вычисленным углом, по их направлениям строим линии.
В данном случае это будет семейство парабол (рис.1).
Некоторые ДУ могут иметь такие решения, которые не получаются из общего ни при каких значениях произвольной постоянной. Эти решения не являются частными и поэтому называются особыми. Особые решения могут иметь только те уравнения, для которых нарушаются условия теоремы существования и единственности решения (теоремы Коши).
Уравнения с разделяющимися переменными (УРП)
Уравнение вида P1(x) Q1 (y) dx + P2(x) Q2 (y) dy = 0 (3)
называется дифференциальным уравнением с разделяющимися переменными (УРП).
Разделив уравнение (3) на P2(x) Q1(y), получим уравнение с разделенными переменными
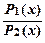 dx +
dx + 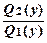 dy = 0(4)
dy = 0(4)
(коэффициент при dx зависит только от х, а при dу – только от у).
Общий интеграл уравнения (4) находится почленным интегрированием:
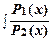 dx +
dx + 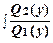 dy = С.
dy = С.
Пример 2. Найти общий интеграл диф.уравнения xdx – ydy = 0.
Имеем: 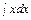 –
– 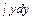 = с1 или
= с1 или 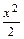 –
– 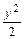 = с2. Обозначим с = 2с2 => x2 – y2 = c.
= с2. Обозначим с = 2с2 => x2 – y2 = c.
Замечание 1.Уравнению (3) могут удовлетворять решения, потерянные при делении на
Q1(y) P2(x), т.е. получаемые из уравнения Q1(y) P2(x) = 0. Если эти решения не
входят в найденный общий интеграл, то они являются особыми решениями ДУ (3).
Замечание 2.Уравнение y¢ = f1(x) f2(у) сводится к уравнению (4), если положить
y¢ = dy/dx и разделить переменные.
Замечание 3.Уравнение y¢ = f (ax + by + c), где a, b, c – числа, путем замены
ax + by + c = u, сводится к диф.уравнению с разделяющимися переменными.
Дифференцируя замену по х, получаем 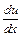 = a + b
= a + b 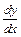 = a + b ∙ f (u) =>
= a + b ∙ f (u) =>  = dx.
= dx.
Интегрируя это уравнение и заменяя u на ax + by + c,получим общий интеграл
исходного уравнения.
Пример 3. Решить уравнение (1 + у2) x dx = (1 + x2) y dy.
Деля обе части уравнения на (1 + у2) (1 + x2) ≠ 0, приведем его к виду 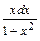 =
= 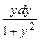 . Интегрируя обе
. Интегрируя обе
части полученного равенства, найдем ln (1 + x2)= ln (1 + y2) + ln C, откуда 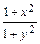 = С.
= С.
Пример 4. Решить уравнение (y + xу) dx + (x – xy) dy = 0.
Деля обе части уравнения на xy ≠ 0, приведем его к виду 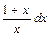 =
= 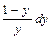 . Интегрируя обе
. Интегрируя обе
части полученного равенства, найдем x + ln | x |= y – ln | y | + C или x + ln | x |– y + ln | y | = C – общий
интеграл уравнения. При делении на ху потеряны решения х = 0 и у = 0, которые также являются
решениями исходного уравнения, но не входят в общий интеграл ни при каком С. Это – особые решения
данного уравнения.
Пример 5. Решить уравнение у dx = х dy.
Разделяя переменные, получим 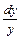 =
= 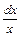 , а после интегрирования ln |y|= ln |x| + ln |C|, откуда у = Сх
, а после интегрирования ln |y|= ln |x| + ln |C|, откуда у = Сх
(здесь С может принимать как положительные, так и отрицательные значения, но С ≠ 0 ).
При делении на у потеряно решение у ≡ 0, которое может быть включено в общее решение, если
разрешить принимать значение С = 0.
Если считать переменные х и у равноправными, то уравнение 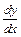 =
=  , теряющее смысл при х = 0, надо
, теряющее смысл при х = 0, надо
дополнить уравнением 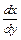 =
= 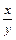 , которое имеет очевидное решение х = 0.
, которое имеет очевидное решение х = 0.
Пример 6. Проинтегрировать уравнение 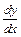 = (х + y)2.
= (х + y)2.
Положим z = x + y, тогда 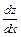 = 1 +
= 1 + 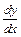 , или
, или 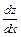 = 1 + z2 , откуда
= 1 + z2 , откуда  = dx. Интегрируя, получим
= dx. Интегрируя, получим
получим arctg z = x + C или z = tg(x + C). Подставляя вместо z величину x + y, получаем общее решение
данного уравнения.
Пример 7. Решить уравнение у′= –  , удовлетворяющее условию у(4) = 1.
, удовлетворяющее условию у(4) = 1.
Имеем: 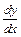 =–
=–  или
или 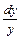 =–
=– 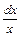 . Проинтегрировав, получим : ln |y|= ln |С| – ln |х|, откуда |у| =
. Проинтегрировав, получим : ln |y|= ln |С| – ln |х|, откуда |у| = 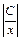 или
или
у = 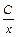 – общее решение ДУ. Подставим в него начальные условия: х = 4, у = 1 и получим: 1 =
– общее решение ДУ. Подставим в него начальные условия: х = 4, у = 1 и получим: 1 = 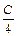 , С = 4.
, С = 4.
Т.о., у =  – частное решение уравнения у′= –
– частное решение уравнения у′= –  . Геометрически это частное решение представляет собой
. Геометрически это частное решение представляет собой
интегральную кривую (в данном случае гиперболу), проходящую через точку (4; 1).
Дата добавления: 2017-11-21; просмотров: 2640;











