Скалярное умножение свободных векторов
О п р е д е л е н и е. Скалярным произведением векторов 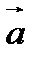 и
и 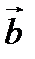 называется число, равное произведению длин этих векторов и косинуса угла между ними:
называется число, равное произведению длин этих векторов и косинуса угла между ними: 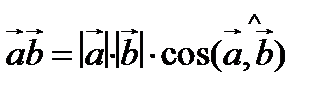 .
.
О п р е д е л е н и е. Векторы, скалярное произведение которых равно нулю называются ортогональными.
Для обозначения ортогональности векторов используют знак 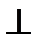 .
.
Очевидны свойства скалярного умножения свободных векторов:
1. 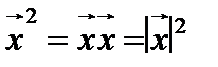 (скалярный квадрат вектора равен квадрату его длины);
(скалярный квадрат вектора равен квадрату его длины);
2. 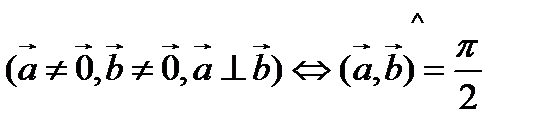 ;
;
3. 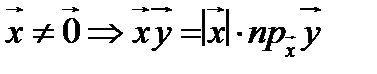 .
.
У п р а ж н е н и е. Используя свойства скалярного умножения и свойства скалярных проекций доказать законы скалярного умножения:
1. 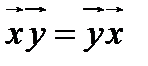 ;
;
2. 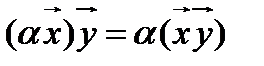 ;
;
3. 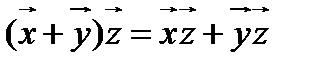 ;
;
4. 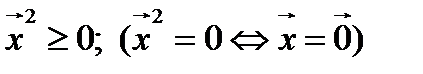 .
.
Базис 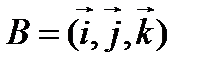 , состоящий из единичных, попарно ортогональных векторов, называется ортонормированным базисом.
, состоящий из единичных, попарно ортогональных векторов, называется ортонормированным базисом.
У п р а ж н е н и е. Используя законы скалярного умножения, вывести формулы вычисления скалярного произведения векторов и длины вектора через координаты в ортонормированном базисе:
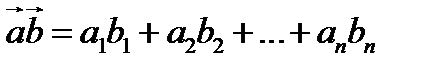 ;
; 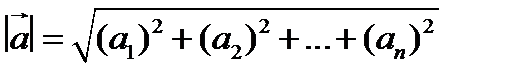 .
.
Основные приложения скалярного умножения векторов:
1. 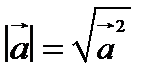 – длина вектора равна корню квадратному из скалярного квадрата этого вектора;
– длина вектора равна корню квадратному из скалярного квадрата этого вектора;
2. 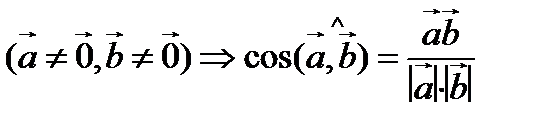 ;
;
3. Угол между векторами 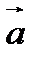 и
и 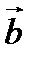 острый тогда и только тогда, когда
острый тогда и только тогда, когда 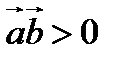 ,тупой тогда и только тогда, когда
,тупой тогда и только тогда, когда 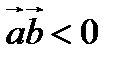 . Векторы
. Векторы 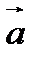 и
и 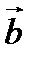 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 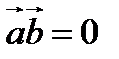 .
.
4. 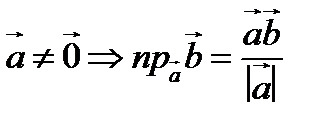 .
.
Дата добавления: 2021-09-25; просмотров: 624;











