Векторное умножение свободных векторов

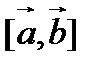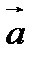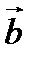О п р е д е л е н и е. Векторным произведением векторов и называется вектор, длина которого равна произведению длин векторов 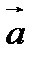и 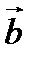на синус угла между ними, этот вектор ортогонален векторам 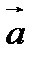и 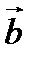и, если он не нулевой, то образует с ними правую тройку.

У п р а ж н е н и е. Найти векторные произведения 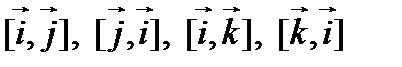векторов ортонормированного базиса .

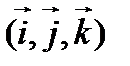Можно сформулировать следующий алгоритм нахождения векторного произведения векторов ортонормированного базиса:

Если порядок сомножителей согласуется с направлением стрелки между этими векторами, то векторное произведение равно оставшемуся вектору. В противном случае, векторное произведение равно вектору, противоположному оставшемуся вектору.

У п р а ж н е н и е. Обосновать свойства векторного умножения свободных векторов:

1. Длина векторного произведения неколлинеарных векторов равна площади параллелограмма, построенного на этих векторах.

2. .

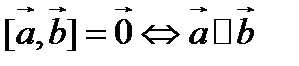3. 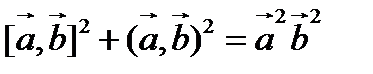(тождество Лагранжа).

Выполняются следующие законы векторного умножения свободных векторов:

1. 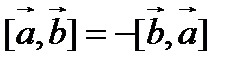(антикоммутативность);

2. 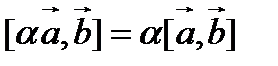(числовой множитель можно выносить за знак векторного умножения);

3. 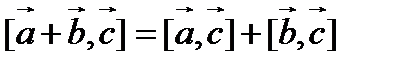(распределительный закон).

Доказательство этих законов рассмотрим в следующем параграфе.

У п р а ж н е н и е. Дайте обоснованные ответы на следующие вопросы:

1. Как, используя векторное произведение векторов, можно найти площадь, высоту параллелограмма, треугольника?