Векторное произведение двух векторов.
Определение. Векторным произведением вектора 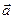 на вектор
на вектор 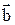 называется вектор
называется вектор

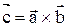 (обозначаемый иначе
(обозначаемый иначе 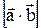 ), удовлетворяющий следующим условиям:
), удовлетворяющий следующим условиям:
1. 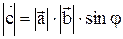 , где j-угол между векторами
, где j-угол между векторами 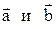 ;
;
2. 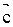 ^
^ 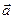 и
и 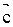 ^
^ 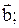
3. 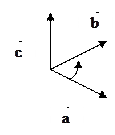 вектор
вектор 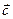 относительно векторов
относительно векторов 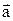 и
и 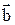 направлен так же, как координатная ось OZ относительно координатных осей OX и OY, т.е. векторы
направлен так же, как координатная ось OZ относительно координатных осей OX и OY, т.е. векторы 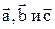 образуют правую тройку векторов (это значит, что если векторы
образуют правую тройку векторов (это значит, что если векторы 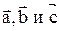 приведены к общему началу, то вектор
приведены к общему началу, то вектор 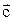 должен быть направлен так, чтобы из его конца наблюдался кратчайший поворот первого вектора ко второму, причем этот поворот осуществлялся бы против хода часовой стрелки:
должен быть направлен так, чтобы из его конца наблюдался кратчайший поворот первого вектора ко второму, причем этот поворот осуществлялся бы против хода часовой стрелки:
Основные свойства векторного умножения:
1. Векторное произведение зависит от порядка сомножителей, т.е.
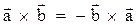 .
.
2. 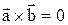 , если
, если 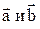 коллинеарны
коллинеарны 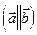 .
.
3. 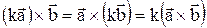 (сочетательный закон).
(сочетательный закон).
4. 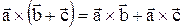 (распределительный закон).
(распределительный закон).
5. 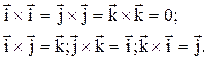
Модуль векторного произведения равен площади S параллелограмма, построенного на векторах 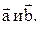
Если векторы 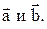 заданы своими координатами
заданы своими координатами
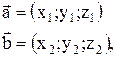
то векторное произведение вектора 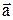 на вектор
на вектор 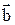 определяется формулой:
определяется формулой:
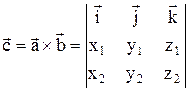 или, (10)
или, (10)
если разложить определитель по элементам первой строки:
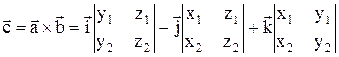 (10/)
(10/)
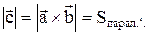 (11)
(11)
Пример 8. Упростить: 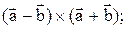
Решение.

Пример 9. Вычислить 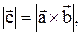 если известно, что
если известно, что 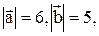 и векторы и векторы
и векторы и векторы 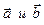 образуют угол j=p/3.
образуют угол j=p/3.
Решение.
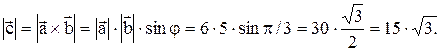
Пример 10. Векторы 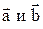 образуют угол j=p/6.
образуют угол j=p/6.
Зная, что 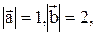 вычислить:
вычислить: 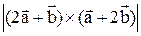 .
.
Решение.
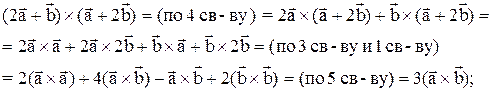
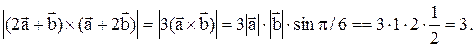
Пример 11. Даны векторы 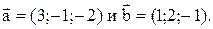
Найти координаты вектора 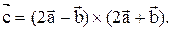
Решение. Найдем координаты векторов-сомножителей:
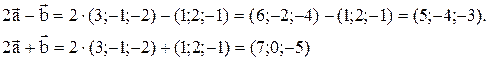
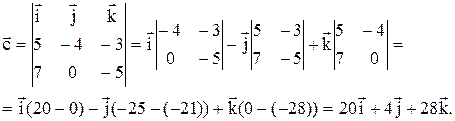
Таким образом вектор 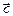 имеет следующие координаты:
имеет следующие координаты:
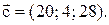
Дата добавления: 2021-11-16; просмотров: 707;











