Проекция вектора на вектор
О п р е д е л е н и е. Единичным вектором или ортом называется вектор, длина которого равна 1.
Если 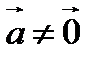 , то вектор
, то вектор 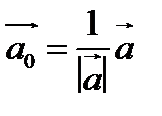 является единичным вектором и называется ортом вектора
является единичным вектором и называется ортом вектора 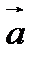 .
.
О п р е д е л е н и е. Проекцией точки 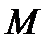 на прямую
на прямую 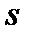 называется точка
называется точка 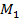 пересечения этой прямой с перпендикулярной ей плоскостью
пересечения этой прямой с перпендикулярной ей плоскостью 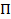 , проходящей через точку
, проходящей через точку 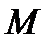 :
: 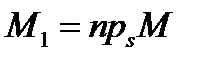 .
.
О п р е д е л е н и е. Векторной проекцией вектора 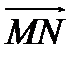 на ненулевой вектор
на ненулевой вектор 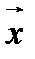 называется вектор
называется вектор 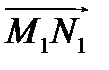 , где
, где 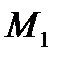 и
и 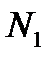 – проекции точек
– проекции точек 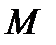 и
и 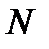 на прямую, параллельную вектору
на прямую, параллельную вектору 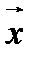 (обозначение
(обозначение 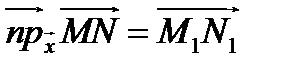 ).
).
Можно показать, что векторная проекция вектора на вектор не зависит от выбора представителя этого вектора.
Так как 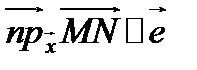 , где
, где 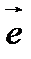 – орт вектора
– орт вектора 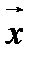 , то
, то 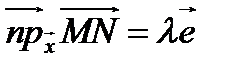 .
.
Число 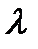 называется скалярной проекцией вектора
называется скалярной проекцией вектора 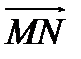 на вектор
на вектор 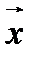 и обозначается
и обозначается 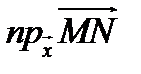 .
.
Таким образом,
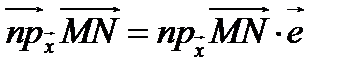
и 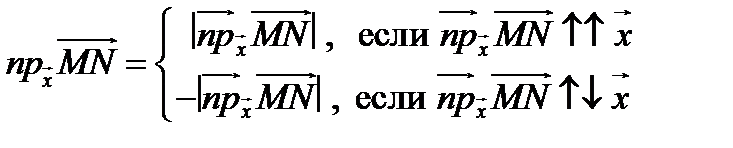 .
.
Отметим, что при определении векторной и скалярной проекций важно только направление ненулевого вектора 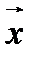 , его длина не является существенной. Таким образом, если
, его длина не является существенной. Таким образом, если 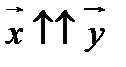 , то
, то 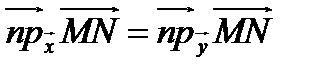 и
и 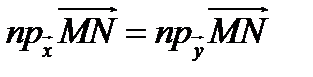 .
.
Можно обосновать следующие свойства векторных проекций:
1. 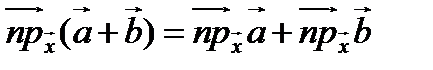 ;
;
2. 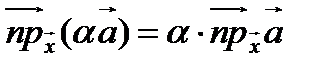 .
.
Выразив векторные проекции через орт вектора 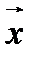 , из свойств векторных проекций получим свойства скалярных проекций:
, из свойств векторных проекций получим свойства скалярных проекций:
1. 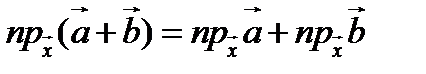 ;
;
2. 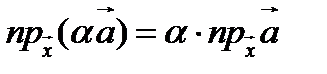 .
.
О п р е д е л е н и е. Углом между ненулевыми свободными векторами 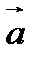 и
и 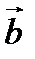 называется величина угла
называется величина угла 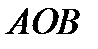 , не превосходящего развернутый угол, где
, не превосходящего развернутый угол, где 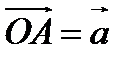 ,
, 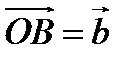 .
.
Таким образом, чтобы увидеть угол между ненулевыми свободными векторами, нужно отложить их от одной точки.
Если один из векторов нулевой, то угол между векторами не определен, можно считать его любым, не превосходящим развернутый угол. Тогда получим, что угол между векторами может принимать значения от 0 до 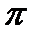 .
.
Рассмотрев возможные значения угла 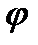 между ненулевыми векторами
между ненулевыми векторами 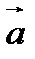 и
и 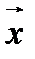
( 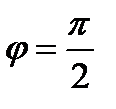 ;
; 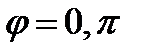 ;
; 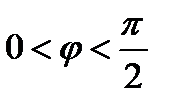 ;
; 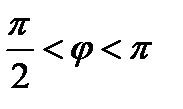 ),
),
получим еще одно свойство скалярных проекций:
3. 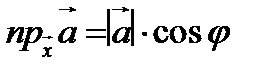 .
.
Дата добавления: 2021-09-25; просмотров: 688;











