Волновая функция свободных электронов в металле
Согласно классическим представлениям валентные электроны атома могут почти свободно перемещаться в пределах образца металла, они обуславливают электропроводимость металла, почему их называют электронами проводимости.
Напомним что классическая электронная теория электропроводности металлов Друде - Лоренца, рассматривая электронный газ в металле как идеальный, успешно объяснила законы Ома, Джоуля – Ленца и Видемана-Франца. Для удельной электропроводности 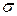 металла в рамках этой теории получается выражение:
металла в рамках этой теории получается выражение:
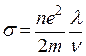 , (38.01)
, (38.01)
где 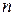 - концентрация электронов проводимости;
- концентрация электронов проводимости;
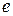 - элементарный заряд;
- элементарный заряд;
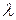 - средняя длина свободного пробега электронов;
- средняя длина свободного пробега электронов;
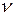 - скорость теплового движения электронов.
- скорость теплового движения электронов.
Одно из основных затруднений классической электронной теории металлов связано температурной зависимостью 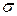 , которая теоретически определяется зависимостью тепловой скорости электронов от температуры. Теория предсказывает зависимость
, которая теоретически определяется зависимостью тепловой скорости электронов от температуры. Теория предсказывает зависимость 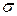 ~
~ 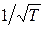 , в то время как экспериментально наблюдается зависимость
, в то время как экспериментально наблюдается зависимость 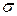 ~
~ 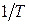 .
.
Второе затруднение заключается в том, что идеальный газ свободных электронов теоретически должен увеличивать молярную теплоемкость металлов на 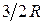 , чего экспериментально не наблюдается.
, чего экспериментально не наблюдается.
Эти затруднения удалось преодолеть квантовой теории свободных электронов, которая рассматривает электронный газ с учетом квантовых свойств электронов и особенностей поведения квантовых систем.
Предположим для простоты и определенности, что образец металла имеет формулу куба со стороной 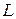 . Допустим, что потенциальная энергия электронов всюду в пределах рассматриваемого образца постоянна и положим её равной нулю:
. Допустим, что потенциальная энергия электронов всюду в пределах рассматриваемого образца постоянна и положим её равной нулю: 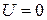 .
.
Тогда уравнение Шредингера для электрона проводимости в металле можно записать в виде:
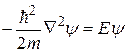 , (38.02)
, (38.02)
Решение уравнения (38.02) имеет вид:
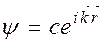 , (38.03)
, (38.03)
где 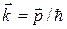 - волновой вектор электрона;
- волновой вектор электрона;
с - константа.
(38.03) есть уравнение плоской волны. Поэтому можно говорить, что электроны в кристалле описываются плоскими волнами. Плоская волна имеет одинаковую во всем объеме кристалла амплитуду. Поскольку квадрат ее модуля дает вероятность обнаружения электрона в данной точке, можно утверждать, что в рамках рассматриваемой модели вероятность обнаружить электрон в любой точке кристалла одинакова.
Электрон с импульсом 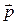 и волновым вектором
и волновым вектором 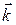 характеризуется кинетической энергией
характеризуется кинетической энергией
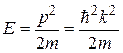 . (38.04)
. (38.04)
Условие нормировки 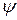 - функции в данном случае можно записать так:
- функции в данном случае можно записать так:
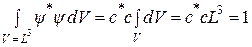 . (38.05)
. (38.05)
Тогда находим значение константы и окончательный вид волновой функции:
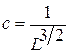 и
и 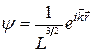 (38.06)
(38.06)
Дата добавления: 2021-01-11; просмотров: 659;











