Выражение смешанного произведения через координаты векторов
Теорема:Если векторы  ,
, 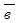 ,
,  заданы своими координатами
заданы своими координатами  ={Х1; У1; Z1 } и
={Х1; У1; Z1 } и  ={Х2 ;У2; Z2 },
={Х2 ;У2; Z2 }, ={Х3; У3; Z3}, то смешанное произведение
={Х3; У3; Z3}, то смешанное произведение  ·
· 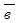 ·
·  определяется формулой
определяется формулой
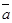 ·
· 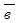 ·
·  =
= 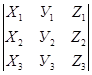 =Х 1
=Х 1 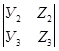 +У1
+У1  +Z1
+Z1 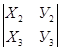 .
.
Доказательство: Имеем: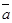 ·
· 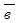 ·
·  =
=  · (
· ( 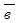 ´
´  ) . По теореме о выражении векторного произведения через координаты векторов
) . По теореме о выражении векторного произведения через координаты векторов 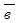 ´
´  =
= 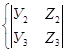 ;
; 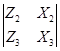 ;
; 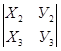
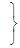 .
.
Умножая скалярно вектор  ={Х1 ;У1; Z1 } на вектор
={Х1 ;У1; Z1 } на вектор 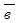 ´
´  и используя теорему о выражении скалярного произведения через координаты получаем
и используя теорему о выражении скалярного произведения через координаты получаем
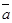 ·
· 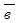 ·
·  = Х1
= Х1 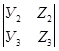 + У1
+ У1  + Z1
+ Z1 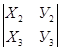 . g
. g
Пример.В пространстве даны четыре точки: А(1; 1; 1), В(4; 4; 4), С (3; 5 ; 5 ), D(2; 4; 7). Найти объем пирамиды, с вершинами в данных точках.
Решение. Как известно из элементарной геометрии, объем тетраэдра АВСD равен одной шестой объема параллелепипеда, построеного на векторах 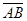 ,
, 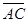 ,
,  ; отсюда из теоремы о смешанном произведении заключаем, что объем тетраэдра равен
; отсюда из теоремы о смешанном произведении заключаем, что объем тетраэдра равен 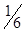 абсолютной величины смешанного произведния
абсолютной величины смешанного произведния 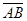 ·
· 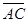 ·
·  . Найдем это смешанное произведение. Прежде всего, определим координаты векторов
. Найдем это смешанное произведение. Прежде всего, определим координаты векторов 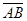 ;
; 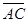 ;
;  . Для этого из координат конца вектора вычесть координаты начала:
. Для этого из координат конца вектора вычесть координаты начала: 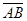 = {3; 3; 3},
= {3; 3; 3}, 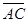 ={2; 4; 4},
={2; 4; 4},  = {1; 3; 6}. Используя теорему о смешанном произведении, получаем
= {1; 3; 6}. Используя теорему о смешанном произведении, получаем 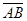 ·
· 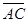 ·
·  = 3
= 3 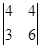 + 3
+ 3 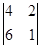 + 3
+ 3 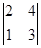 = 3 · 12 – 3 · 8 + 3 · 2 = 18. Отсюда V =
= 3 · 12 – 3 · 8 + 3 · 2 = 18. Отсюда V = 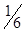 · 18 = 3 куб. ед.
· 18 = 3 куб. ед.
Аксиоматические построения и система аксиом
Дата добавления: 2022-02-05; просмотров: 561;











