Внутреннее, или скалярное произведение векторов

Скалярное произведениедвух векторов x и y одинаковой размерности (n×1) обозначается <x, y> и определяется в общем случае комплексных x, y следующим образом:

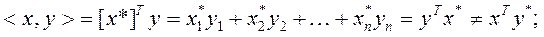
для действительных векторов x и y:

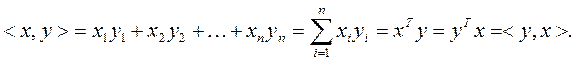
О р т о г о н а л ь н ы е в е к т о р ы

Два вектора называются ортогональными, если их скалярное произведение <x, y>равно нулю:

<x , y> = 0 .

Внешнее, или векторное произведение векторов

Если вектор-столбец x размерности (m×1) обозначить через x>, а вектор-строку [y*]^T размерности (1×n) обозначить через <y, то внешним произведениемx><y будет матрица (m×n):

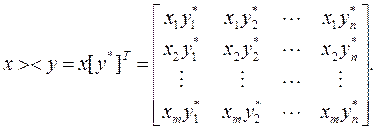
Длина вектора

В общем случае длина вектора x, называемая также нормой, определяется следующим образом:

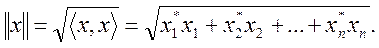
Для действительных x:

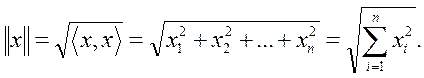
Неравенства

2.5.4.1. Неравенство треугольника:

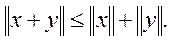
2.5.4.2. Неравенство Шварца:

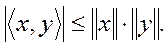
Единичный вектор– вектор, длина (норма) которого равна единице:

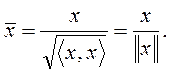
Линейная независимость векторов

Векторы x_i(i=1, 2, 3, …, m) называются линейно независимыми, если не существует постоянных величин k_i (i=1, 2, 3,…, m), из которых хотя бы одна отлична от нуля, так что можно было бы записать:

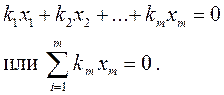
Особенная матрица

Если строки или столбцы матрицы не являются линейно-независимыми, в этом случае определитель этой матрицы равен нулю.