Линейно зависимые системы векторов

Произвольный набор векторов 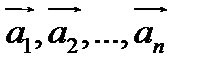векторного пространства называют системой векторов.

Для системы векторов можно составлять бесконечно много линейных комбинаций, то есть выражений вида .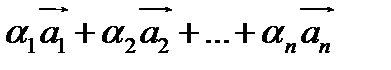

О п р е д е л е н и е. Линейная комбинация, в которой все коэффициенты 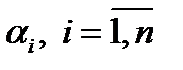равны нулю, называется тривиальной линейной комбинацией.

Очевидно, тривиальная линейная комбинация всегда равна 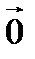. Однако может случиться, что и нетривиальная линейная комбинация векторов равна 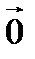. Например, пусть 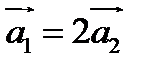. Тогда нетривиальная линейная комбинация 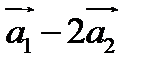равна .

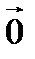О п р е д е л е н и е. Система векторов называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная .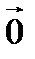

Если же не существует нетривиальной линейной комбинации векторов, равной 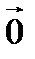, то есть 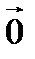можно получить только в результате тривиальной линейной комбинации, то система векторов называется линейно независимой.

У п р а ж н е н и е. Доказать условие линейной зависимости системы из 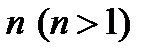векторов:

Т е о р е м а 1. При 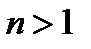система векторов линейно зависимая тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов системы.

У п р а ж н е н и е. Доказать теоремы, раскрывающие геометрический смысл линейной зависимости системы из 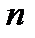свободных векторов:

Т е о р е м а 2. Система, состоящая из одного свободного вектора линейно зависимая тогда и только тогда, когда этот вектор нулевой.

Т е о р е м а 3. Система из двух свободных векторов линейно зависимая тогда и только тогда, когда эти векторы коллинеарны.

Т е о р е м а 4. Система из трех свободных векторов линейно зависимая тогда и только тогда, когда эти векторы компланарны.

Т е о р е м а 5. Всякие четыре свободных вектора образуют линейно зависимую систему векторов.