Ориентация векторного пространства

Рассмотрим трехмерное векторное пространство 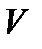, образованное всеми свободными векторами геометрического пространства.

Т е о р е м а. (условие компланарности трех векторов). Три вектора компланарны тогда и только тогда, когда определитель третьего порядка, составленный из координат этих векторов равен нулю.

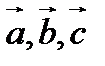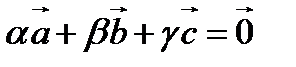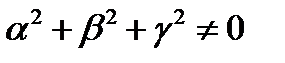Д о к а з а т е л ь с т в о. Векторы компланарны тогда и только тогда, когда система этих векторов является линейно зависимой, то есть существует нетривиальная линейная комбинация этих векторов, равная : , где . Записав это условие в координатах, получим систему трех линейных однородных уравнений

.

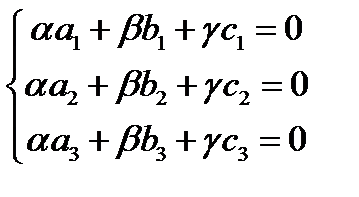Эта система имеет ненулевое решение 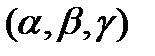, следовательно, её определитель равен нулю.

В пространстве 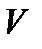существует бесконечное множество базисов. Пусть 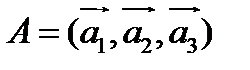и 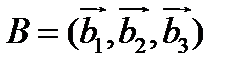два базиса. Векторы базиса 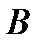можно выразить через векторы базиса :

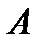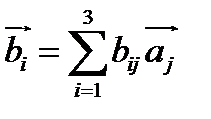
Матрица 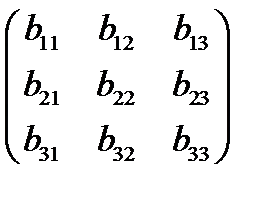, составленная из координат векторов 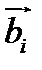, называется матрицей перехода от базиса к базису .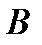

Обозначим 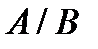определитель этой матрицы. Так как векторы 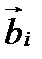некомпланарны, то .

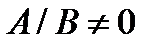Непосредственными вычислениями можно проверить, что:

1. ;

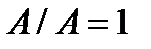2. .

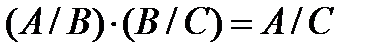Обозначим Вмножество всех базисов в пространстве . Будем говорить, что два базиса и 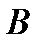ориентированы одинаково 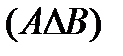, если 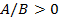. Очевидно, что:

1. ;

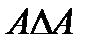2. ;

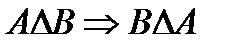3. .

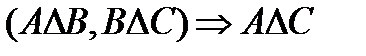Таким образом, отношение (быть одинаково ориентированными) на множестве В всех базисов пространства является отношением эквивалентности. Множество В всех базисов разбивается на классы эквивалентности. Каждый класс состоит из всех одинаково ориентированных между собой базисов.

Т е о р е м а. Отношение разбивает множество В ровно на два класса эквивалентности.

Д о к а з а т е л ь с т в о. Рассмотрим два базиса: 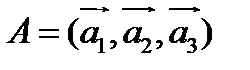и 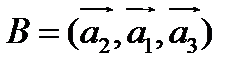. Тогда 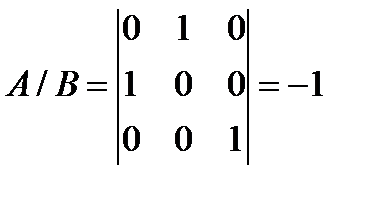. Следовательно, базисы 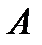и 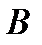не являются одинаково ориентированными, то есть принадлежат разным классам эквивалентност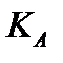и и 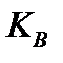. Для любого другого базиса 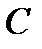будем иметь

.

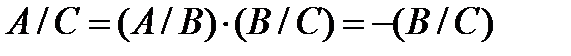То есть, либо 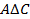, либо 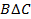и, следовательно, либо 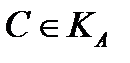, либо 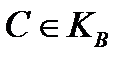. Таким образом получаем ровно два класса эквивалентности для отношения .

О п р е д е л е н и е. Каждый из классов эквивалентности отношения (быть одинаково ориентированными) называется ориентацией пространства 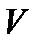. Одна из них называется положительной или правой, другая отрицательной или левой.

Если тройка векторов 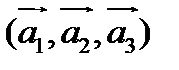принадлежит правой (левой) ориентации, то её называют правой (левой) тройкой векторов.

При циклической перестановке векторов ориентация тройки не меняется. Если два соседних вектора поменять местами, ориентация тройки меняется.

Внематематическое соглашение: тройку векторов 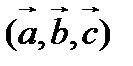будем считать правой, если со стороны вектора 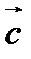видно, что поворот от 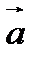к 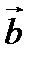совершается против часовой стрелки.