Смешанное умножение свободных векторов
О п р е д е л е н и е. Смешанным произведением 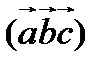 свободных векторов
свободных векторов 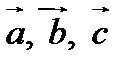 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 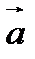 и векторного произведения
и векторного произведения 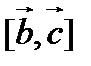 .
.
Следующие две теоремы раскрывают геометрический смысл смешанного произведения трех свободных векторов.
Т е о р е м а 1 (условие компланарности трех векторов). Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Т е о р е м а 2 (о геометрическом смысле смешанного произведения трех некомпланарных векторов). Смешанное произведение трех некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка векторов левая.
У п р а ж н е н и е. Дайте обоснованные ответы на следующие вопросы:
1. Как, используя векторное и смешанное произведение векторов, можно найти объем, высоту параллелепипеда, тетраэдра?
У п р а ж н е н и е. Опираясь на определение и геометрический смысл смешанного произведения трех векторов, а так же на законы скалярного умножения, докажите законы смешанного умножения векторов:
1. 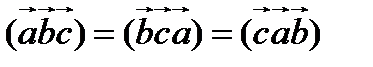 (при циклической перестановке сомножителей смешанное произведение не меняется);
(при циклической перестановке сомножителей смешанное произведение не меняется);
2. 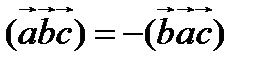 (при перестановке двух соседних сомножителей смешанное произведение меняет свой знак);
(при перестановке двух соседних сомножителей смешанное произведение меняет свой знак);
3. 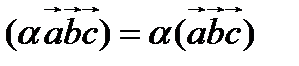 (числовой множитель можно выносить за знак смешанного умножения);
(числовой множитель можно выносить за знак смешанного умножения);
4. 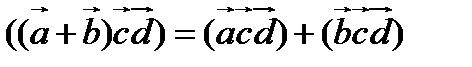 (распределительный закон).
(распределительный закон).
Для доказательства законов векторного умножения воспользуемся законами смешанного умножения и следующей леммой.
Л е м м а. Если для любого вектора 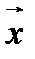 скалярное произведение
скалярное произведение 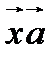 равно нулю, то вектор
равно нулю, то вектор 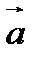 – нулевой вектор.
– нулевой вектор.
Чтобы убедиться в справедливости леммы, достаточно в качестве 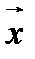 взять вектор
взять вектор 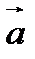 .
.
Докажем закон антикоммутативности векторного умножения. Для любого вектора 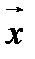 имеем
имеем 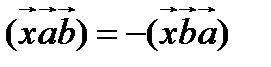 или
или 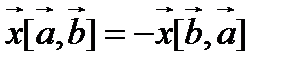 . Используя законы скалярного умножения, получим
. Используя законы скалярного умножения, получим 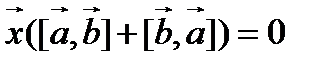 . Тогда по лемме следует, что
. Тогда по лемме следует, что 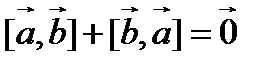 . Имеем
. Имеем 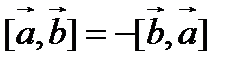 .
.
Остальные законы векторного умножения доказываются аналогично.
У п р а ж н е н и е. Укажите, какие свойства и законы скалярного, векторного и смешанного умножений используются на каждом этапе вывода формул вычисления векторного и смешанного произведений через координаты в ортонормированном базисе 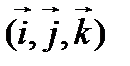 :
:
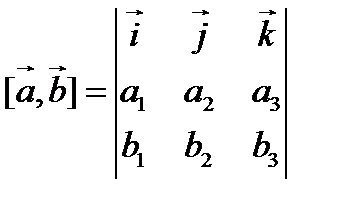 ,
, 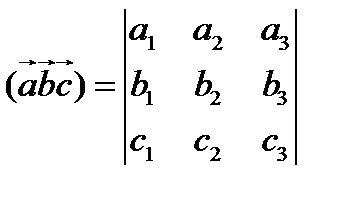 .
.
Раздел II. Аналитическая планиметрия
Дата добавления: 2021-09-25; просмотров: 578;











