Сложение и вычитание свободных векторов
О п р е д е л е н и е. Сумма свободных векторов 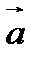 и
и 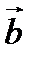 определяется по «правилу треугольника»:
определяется по «правилу треугольника»:
Отложим от точки 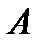 вектор
вектор 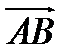 , равный вектору
, равный вектору 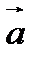 . От точки
. От точки 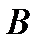 отложим вектор
отложим вектор  , равный вектору
, равный вектору 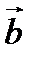 . Вектор
. Вектор 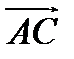 назовем суммой векторов
назовем суммой векторов  и
и  .
.
У п р а ж н е н и е.Доказать теорему о независимости суммы свободных векторов от выбора начальной точки  .
.
Из определения суммы векторов следует свойство:
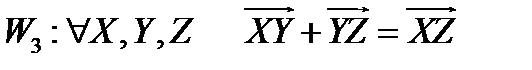 (аксиома треугольника).
(аксиома треугольника).
У п р а ж н е н и е.Доказать законы сложения векторов:
1. 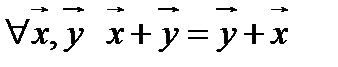 (переместительный закон или коммутативность);
(переместительный закон или коммутативность);
2. 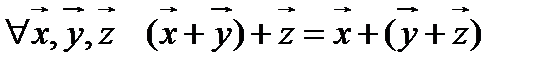 (сочетательный закон или ассоциативность);
(сочетательный закон или ассоциативность);
3. 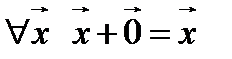 ;
;
4. 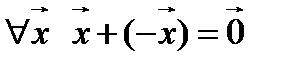 .
.
О п р е д е л е н и е. Разностью свободных векторов 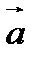 и
и 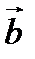 называется такой вектор
называется такой вектор 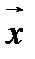 , что
, что 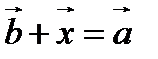 .
.
Прибавив к обеим частям равенства 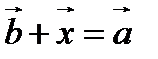 вектор
вектор  , получим
, получим 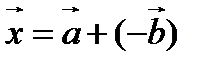 . Таким образом, чтобы вычесть из вектора
. Таким образом, чтобы вычесть из вектора 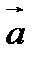 вектор
вектор 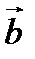 , нужно к
, нужно к  прибавить вектор, противоположный вектору
прибавить вектор, противоположный вектору  .
.
Полезно запомнить, что если два вектора отложены от одной точки, то вектор, соединяющий их концы, является разностью этих векторов. Причем из того вектора, где сходятся две стрелочки, вычитают второй вектор: 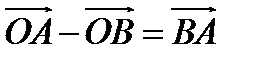 .
.
Дата добавления: 2021-09-25; просмотров: 569;











