Умножение свободного вектора на число

О п р е д е л е н и е. Произведением свободного вектора 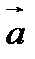на действительное число 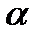называется свободный вектор 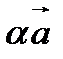, длина которого равна произведению модуля числа 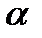на длину вектора 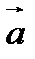, и этот вектор сонаправлен с вектором 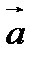, если число 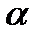неотрицательное, и противоположно направлен, если число 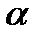отрицательное:

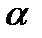
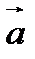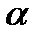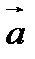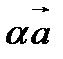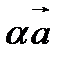∣ ∣=∣ ∣ ∣ ∣, ⇈ , если 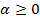, 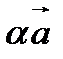⇅ 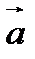, если .

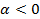У п р а ж н е н и е.Доказать законы умножения вектора на число:

5. ;

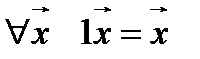6. ;

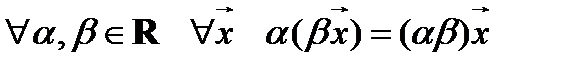7. ;

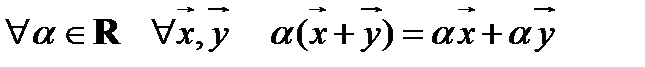8. ;

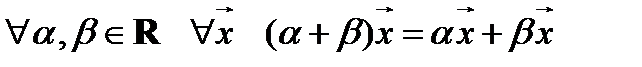У п р а ж н е н и е. Доказать условие коллинеарности двух векторов:

Два вектора коллинеарны тогда и только тогда, когда они отличаются друг от друга числовым множителем.

О п р е д е л е н и е. Выражение 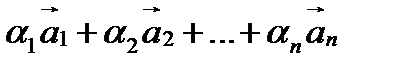называют линейной комбинацией векторов .

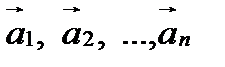Ясно, что результатом линейной комбинации векторов является вектор.

Доказанные законы сложения векторов и умножения вектора на число, позволяют применять к линейным комбинациям векторов все правила преобразований, установленные в алгебре для многочленов первой степени. Можно приводить подобные; раскрывать скобки; выносить за скобку; переносить с противоположным знаком из одной части равенства в другую; умножать обе части равенства на одно и то же число.