Б. Сложение колебаний с разными частотами.

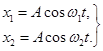Þx = x₁ + x₂ = A[cosw₁t+cosw₂t]. (5.8)

Из формул тригонометрии

cosa + cosb = 2cos 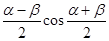. (5.9)

Значит: x = x₁ + x₂ = 2Acos 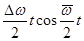. (5.10)

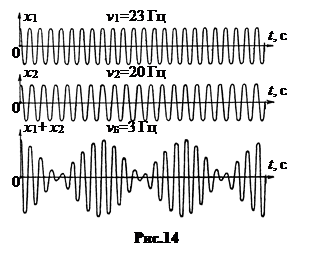
Суммарное колебание точки можно толковать как условно гармоническое с частотой 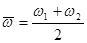и медленно изменяющейся амплитудой (рис.14).

Частоту пульсации амплитуды называют частотой биений, Dw = |w₁ - w₂|.

4. Сложение взаимно перпендикулярных колебаний. Точка колеблется одновременно в двух перпендикулярных направлениях. Возможны два случая: частоты колебаний одинаковы и частоты колебаний различны.

а. Частоты колебаний одинаковы.

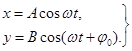(5.11)

Исключив время t, найдем уравнение траектории.

Из первого уравнения: cosw t = 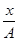; sinw t = 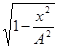. Подставив во второе:

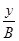=cosw t·cosj₀ - sinw t·sinj₀ = 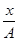cosj₀ - 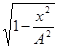·sinj₀.

Избавившись от корня, получаем: 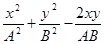cosj₀ = sin²j_0. (5.12)

Это уравнение эллипса.

В зависимости от начальной фазы выделяют наиболее характерные случаи:

j₀ = 0, j₀ = ± 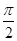, j₀ = ±p.

j₀ = 0 (рис.15). 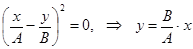. (5.13)

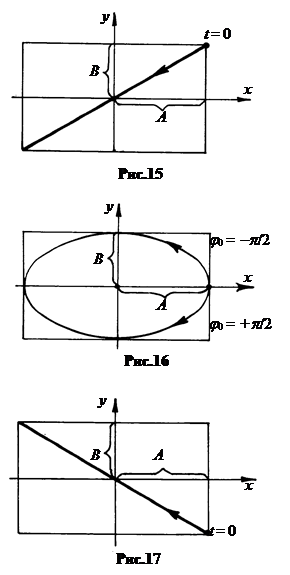Расстояние от колеблющейся точки до центра СК есть r = .

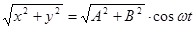Следовательно, колебание точки в данном случае происходит вдоль прямой и также является гармоническим.

j₀ = ±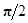(рис.16). Уравнение траектории в этом случае: 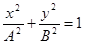. (5.14)

Оси эллипса совпадают по направлению с осями координат. При А = В эллипс вырождается в окружность. 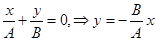. (5.15)

j₀ = ±p(Рис.17). В отличие от первого случая траектория проходит через второй и четвертый квадранты СК.

б. Частоты колебаний различны. Если частоты относятся как целые числа, w₁:w₂ = 1,2,3,¼ 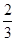,¼ то траектория замкнута, движение периодическое. Такие траектории называются фигурами Лиссажу (рис.18).

Если отношение частот нельзя представить отношением целых чисел, то траектория не замкнута, она постепенно заполняет весь прямоугольник со сторонами 2А и 2В.

Заключение. Можно спросить: сколько кинематических характеристик исчерпывающе определяют механическое движение тел? Так как скорость и ускорение – это первая и вторая производные от пути по времени, то вопрос можно поставить иначе: до какого максимального порядка следует находить производные от пути по времени, чтобы полностью описать механическое движение? Так ли уж нужно было вводить вторую производную от пути по времени - ускорение? И не потребуется ли ввести в дифференциальные уравнения движения третью или четвертую производные?..

Необходимое для полного описания состояния движения материальной точки количество кинематических характеристик определяется свойствами пространства-времени. Из однородности времени вытекает закон сохранение энергии, что требует введения понятия скорости 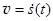. Однородность и изотропность пространства дают законы сохранения импульса и момента импульса, пропорциональные скорости движения точки. Таким образом, все механические состояния точки можно описать, задавая 3 координаты и 3 проекции скорости точки на оси координат, т.е. 6 независимых начальных параметров

Как установил ещё Ньютон, причиной изменения состояния движения материальной точки является сила. Поэтому в дифференциальные уравнения движения точки должны входить все кинематические характеристики, от которых зависят силы. Современная физика в большинстве случае имеет дело с силами, зависящими от координат и скоростей точки, и только в случае излучения - с силами, зависящими от ускорений.

Можно допустить, что будут открыты новые свойства пространства-времени, которые потребуют для описания каких-то механических взаимодействий производных более высоких порядков. Однако на сегодня такие свойства неизвестны, и потому для полного описания движения материальной точки достаточно знания дифференциальных уравнений её движения не выше второго порядка и начальных условий.