Алгебраическое сложение/вычитание чисел в прямом коде
Пример:
С = А ± В, где:
А и В целые числа со знаком, представленные в прямом коде.
Для исключения действия "вычитание", перед выполнением операции исходные числа переводятся из прямого кода в дополнительный или обратный код. Следовательно, операция алгебраического сложения/вычитания состоит из следующей цепочки последовательных действий:
· проверка знака первого операнда; если первый операнд отрицательный, то формируют его представление в дополнительном или обратном коде,
· проверка знака второго операнд; если второй операнд отрицательный, то формируют его представление в дополнительном или обратном коде,
· проверка кода операции; если операция вычитания, то меняют знак второго операнда и снова формируют его представление в дополнительном или обратном коде.
Эту цепочку действий можно модифицировать.
Рассмотрим все возможные комбинации знаков чисел и действий и сделаем ряд преобразований, так чтобы знак результата совпадал со знаком первого операнда:
1. А + В = + (А + В)
2. А + (– В) = + (А – В)
3. (– А) + В = – (А – В)
4. (–А) + (–В) = – (А + В)
5. А – В = + (А – В)
6. А – (– В) = + (А + В)
7. (– А) – В = – (А + В)
8. (– А) – (– В) = – (А – В)
В этом случае алгоритм алгебраического сложения вычитания чисел в прямом коде можно записать в виде последовательности следующих действий:
· сравнение знаков операндов. Если знаки операндов разные, то арифметическое действие заменяется обратным (вычитание – сложением, а сложение – вычитанием),
· выполняют арифметическое действие выполнение арифметического действия: при сложении суммируются абсолютные значения слагаемых, при вычитании формируется отрицательное значение второго операнда в дополнительном коде и производится его суммирование с первым операндом. В обоих случаях результату присваивается знак первого слагаемого. При выполнении вычитания в случае, когда первое слагаемое первый операнд меньше (по абсолютному значению) второго по абсолютному значению, отсутствует единица переноса из старшего разряда и результат получается в виде отрицательного числа в дополнительном коде.
· При отсутствии переноса из старшего разряда, для представления результата в прямом коде все разряды результата, включая знаковый, инвертируется и к младшему разряду прибавляется единица.
Для более наглядной и краткой записи алгоритмов можно использовать их запись в форме блок-схем блок-схемы.
Алгоритм алгебраического сложения/вычитания чисел в прямом коде можно записать в виде блок-схемы, представленной на рис. 5.1.
В блок схеме используются два типа блоков:
· Блоки выполнения действия над значениями исходных переменных с присваиванием результата новым переменным или одной из старых. Эти блоки изображаются в виде прямоугольных рамок с текстом, задающим эти действия;
· Блоки ветвлений с указаниями проверок условий ветвлений. Эти блоки изображаются в виде ромбических рамок с указаниями условий ветвлений (переходов).
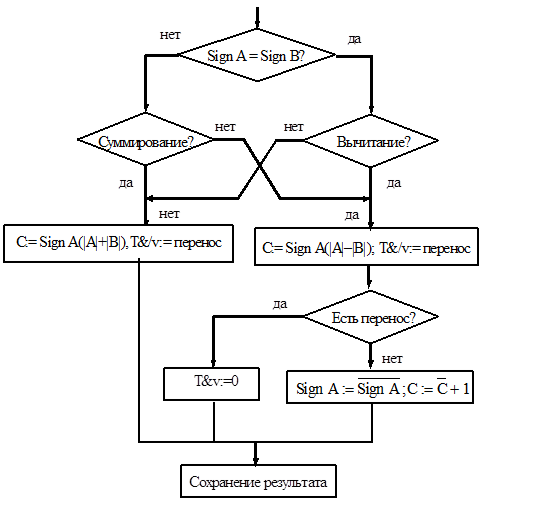
Рис. 5.1. Блок схема алгоритма выполнения алгебраического сложения / вычитания чисел в прямом коде
T&/V
триггер кода операции/переполнения T&/v
Дата добавления: 2022-02-05; просмотров: 869;











