ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.

Дифференциальное уравнение вида

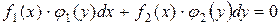(1)

в котором коэффициенты пр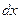и и 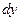представляют собой производные двух непрерывных функций из которых одна зависит от одной, вторая от другой переменной, называется дифференциальным уравнением с разделяющимися переменными.

Разделим обе части дифференциального уравнения (1) на произведение членов, “мешающих” соответственно интегрированию по 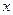и 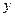, т.е. на 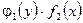. В результате получим дифференциальное уравнение с разделенными переменными:

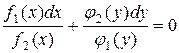
Интегрируя почленно это уравнение, получим общий интеграл уравнения (3.1):

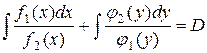
Деление на 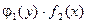- может привести к потере частных (особых) решений уравнения (3.1), обращающих в ноль произведение .

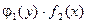Пример.Найти частное решение дифференциального уравнения.

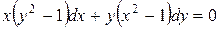
Решение.Разделим переменные, для чего делим обе части уравнения на 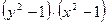, получим:

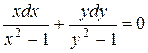
Интегрируем все части уравнения:

,

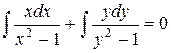
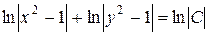упростим 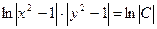, или, потенцируя .

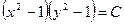Для простоты записи окончательного результата нам было удобно написать постоянную интеграции в виде .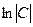

Пример.

Найти решение дифференциального уравнения .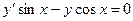

Решение.Так как 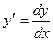, имеем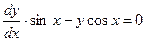

Умножив обе части равенства на 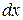, получим .

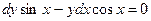Это уравнение с разделяющимися переменными вида (1), потому делим все слагаемые на 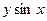. При этом мы полагаем, что 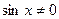и 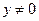. В результате преобразований имеем: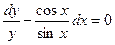

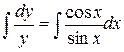
Интегрируя, получаем , .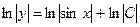

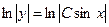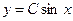- общее решение.

При делении на произведение 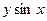возможна потеря решений дифференциального уравнения, обращающих это произведение в нуль. К таким решениям относятся 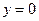и 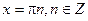. Однако 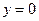входит в общее решение (при 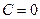), а 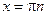не является решением исходного уравнения вообще. Таким образом, все решения уравнения .

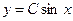Пример.

Найти частное решение дифференциального уравнения 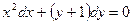, удовлетворяющее начальным условиям .

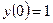Решение.

Интегрируя уравнение почленно, получаем общий интеграл уравнения

,

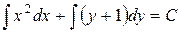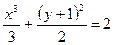или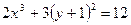

Все дальнейшие методы решения дифференциальных уравнений первого порядка будут состоять в искусстве сведения этих уравнений к уравнению с разделяющимися переменными.