ИНТЕГРАЛЫ ОТ НЕПРЕРЫВНЫХ ФУНКЦИЙ

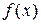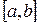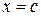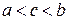а) Пусть непрерывна во всех точках отрезка за исключением точки , где , тогда:

.

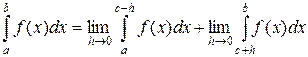б) Пусть 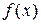непрерывна во всех точках отрезка 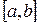за исключением точки 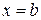, тогда:

.

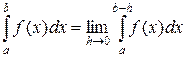в) Пусть 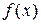непрерывна во всех точках отрезка 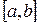за исключением точки 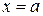, тогда:

.

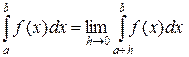г) Пусть 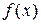непрерывна во всех точках отрезка 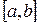за исключением точек 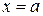и 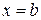, тогда:

.

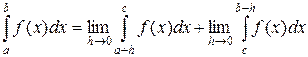Эти интегралы могут как сходиться, так и расходиться.

Пример. Исследовать интеграл на сходимость .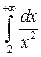

Решение.

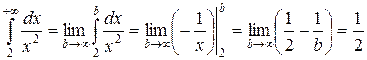– интеграл сходится.

Пример. Исследовать интеграл на сходимость .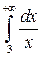

Решение.

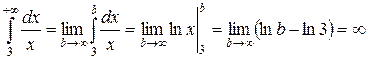– интеграл расходится.

Пример. Исследовать интеграл на сходимость .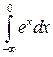

Решение.

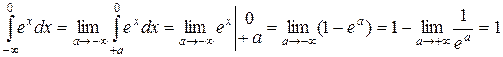– сходится.

Пример. Исследовать интеграл на сходимость .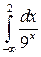

Решение.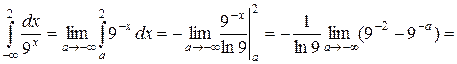

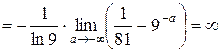– расходится.

Пример. Исследовать интеграл на сходимость .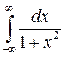

Решение.

.

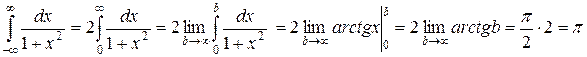Пример. Исследовать интеграл на сходимость .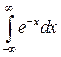

Решение.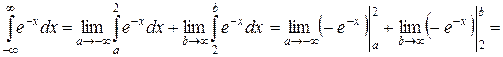

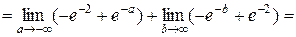
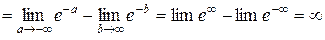– интеграл расходится.

Пример. Исследовать интеграл на сходимость .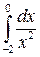

Решение.

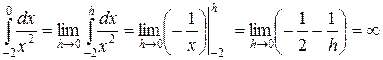– интеграл расходится.

Пример. Исследовать интеграл на сходимость .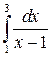

Решение.

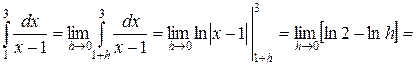
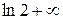– расходится.

Пример. Исследовать интеграл на сходимость .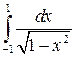

Решение.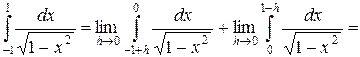

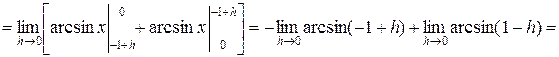
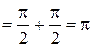– сходится.

Пример. Исследовать интеграл на сходимость .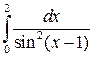

Решение.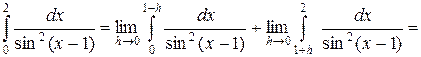

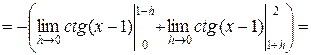
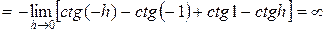– интеграл расходится.

Пример. Исследовать интеграл на сходимость .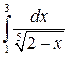

Решение.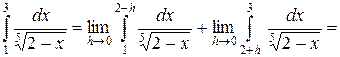

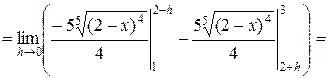
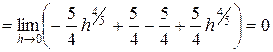– интеграл сходится.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое определенный интеграл?

2. Назовите основные свойства определенного интеграла.

3. Сформулируйте формулу Ньютона-Лейбница.

4. Что такое интегральная сумма функции.

5. Что называется несобственным интегралом с бесконечной верхней границей?

6. Что называется несобственным интегралом с бесконечной нижней границей?

7. Что называется несобственный интеграл с двумя бесконечными границами?