ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
Определение интеграла, приведенное в п. 2.1, было дано в предположении, что областью интегрирования является конечный промежуток 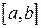 . Если же предположить, что область интегрирования бесконечна, например, является интервалом
. Если же предположить, что область интегрирования бесконечна, например, является интервалом 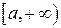 , то даже для непрерывной функции
, то даже для непрерывной функции 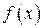 обычное определение интеграла становится неприемлемым. В данном случае нельзя говорить об интегральных суммах, так как при любом разбиении интервала
обычное определение интеграла становится неприемлемым. В данном случае нельзя говорить об интегральных суммах, так как при любом разбиении интервала 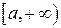 на конечное число частей одна из этих частей будет бесконечной.
на конечное число частей одна из этих частей будет бесконечной.
Если интеграл 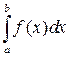 стремится к конечному пределу при неограниченном возрастании
стремится к конечному пределу при неограниченном возрастании 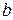 , то этот предел называют несобственным интегралом с бесконечной верхней границей от функции
, то этот предел называют несобственным интегралом с бесконечной верхней границей от функции 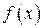 и обозначают символом
и обозначают символом 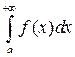 .
.
Таким образом, 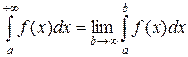 .
.
В этом случае говорят, что несобственный интеграл существует или сходится. Если указанный предел не существует (в частности, если он бесконечен), то говорят, что интеграл не существует или расходится.
Аналогично определяется несобственный интеграл с бесконечной нижней границей:
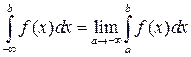 .
.
Несобственный интеграл с двумя бесконечными границами определяется формулой
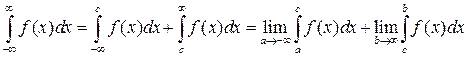 ,
,
где 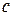 – любая фиксированная точка оси
– любая фиксированная точка оси 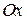 .
.
Таким образом, интеграл 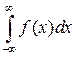 существует тогда и только тогда, когда существует каждый из интегралов
существует тогда и только тогда, когда существует каждый из интегралов 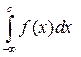 и
и 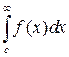 .
.
Дата добавления: 2021-09-25; просмотров: 468;











