МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Формула интегрирования по частям имеет вид

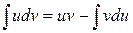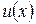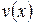где и – дифференцируемые функции.

Применение формулы интегрирования по частям основывается на следующем: подынтегральное выражение разбивают на два множителя, один из которых обозначают через 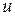, другой через – 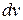. В качестве 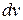следует брать выражение, от которого достаточно легко берется интеграл, за 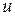– функцию, которая упрощает выражение. Затем по установленному выражению 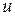дифференцированием найти 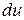, а по известному 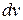путем интегрирования найти функцию 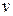(при этом считают, что ).

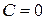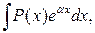
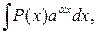
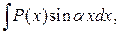
Для интегралов вида 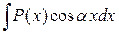, где 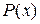- многочлен, за 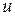следует принять .

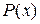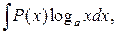
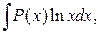
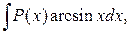
Для интегралов вид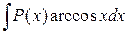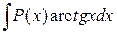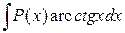а , , за 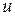принимаются соответственно функции , , , , , .

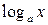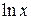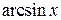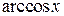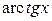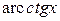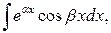
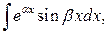
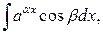
Для интегралов вид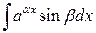а за 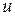можно принять любую из функций, но здесь требуется двукратное интегрирование по частям.

Пример. Вычислить интеграл .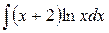

Решение. Полагая 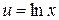, , 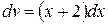имеем 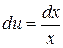, , 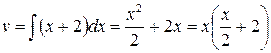следовательно,

.

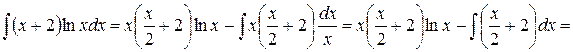
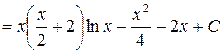Пример. Вычислить интеграл .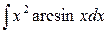

Решение. Полагая 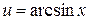, , 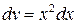имеем 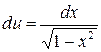, , 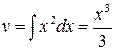следовательно,

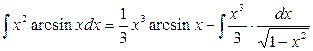. (а)

Теперь найдем интеграл в правой части равенства (а) с помощью подстановки 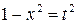. Дифференцируя, получаем 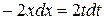или 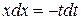, следовательно,

.

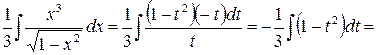
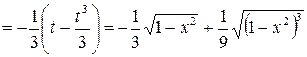Подставляя этот результат в равенство (а), находим

.

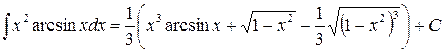Пример. Вычислить интеграл .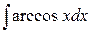

Решение.Данный интеграл представляет собой произведение обратной тригонометрической функции на многочлен нулевой степени. Тогда, для интегрирования по частям, полагая 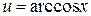, , 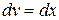имеем 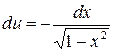, , 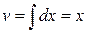следовательно,

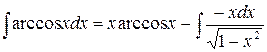. (б)

Интеграл в правой части найдем с помощью подстановки , ;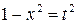

.

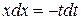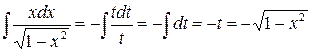Подставляя этот результат в равенство (б), получаем

.

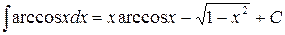Пример. Вычислить интеграл .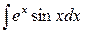

Решение. Для интегрирования по частям, полагая 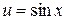, , 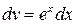имеем 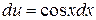, , 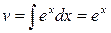следовательно,

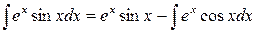. (в)

Интеграл в правой части снова интегрируем по частям. Полагая 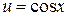, , 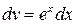имеем 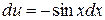, , 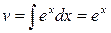следовательно,

.

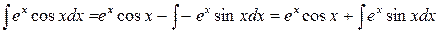Подставляя этот результат в равенство (в), получаем

,

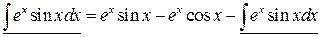приведем подобные элементы

.

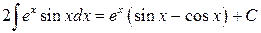Следовательно,

.

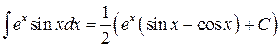Пример. Вычислить интеграл .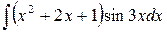

Решение. Для интегрирования по частям, полагая 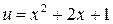, , 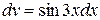имеем 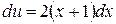, , 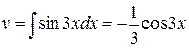следовательно,

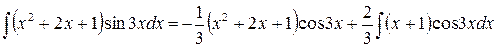. (г)

Интеграл в правой части снова интегрируем по частям. Полагая 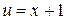, , 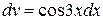имеем 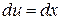, , 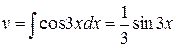следовательно,

.

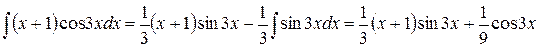Подставляя этот результат в равенство (г), получаем

.

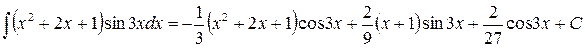Пример. Вычислить интеграл .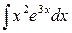

Решение. Полагая 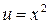, , 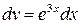имеем 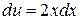, , 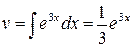следовательно,

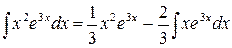. (д)

Вычисляем интеграл в правой части равенства (д) с помощью формулы интегрирования по частям: 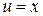, , 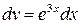, , 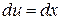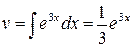следовательно,

.

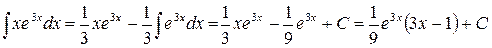Подставляя этот результат в равенство (д), получаем

.

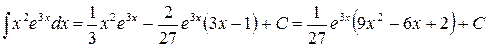Контрольные вопросы

1. Что такое неопределенный интеграл?

2. Что такое первообразная функция?

3. Назовите основные свойства неопределенного интеграла?

4. Назовите формулу интегрирования по частям.

5. Что следует принять за 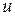для интегралов вида ?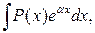

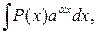
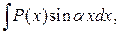
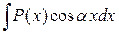6. Что следует принять за 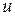для интегралов вида , , ?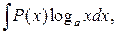

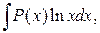
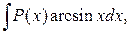
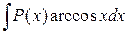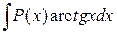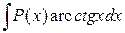<11 12 131415 16 17 >

Дата добавления: 2021-09-25; просмотров: 235;