Вопрос 3. Ток смещения и второе уравнение Максвелла в интегральной форме.

<8 9 101112 13 14 >

Второе уравнение Максвелла в интегральной формеявляется обобщением на переменные поля закона Био – Савара – Лапласа о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только электрическими токами, текущими в проводнике, но и переменными электрическими полями в диэлектриках или вакууме. Чтобы установить количественные соотношения между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Для определения понятия тока смещения рассмотрим цепь переменного тока с напряжением U и подключенным к ней конденсатором С (рис.3.1).

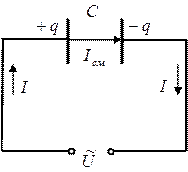
Рис. 3.1.

Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле. Согласно теории Максвелла, в тех участках электрической цепи, где отсутствуют проводники тока, токи проводимости замыкаются токами смещения I_см в диэлектрике конденсатора, причем

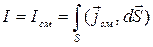, (3.4)

где 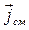- плотность тока смещения.

То есть, переменное электрическое поле в конденсаторе (или ток смещения) в любой момент времени создает такое же магнитное поле, как если бы через конденсатор протекал ток проводимости, равный силе тока в металлических проводниках цепи.

Ток проводимости вблизи обкладок конденсатора можно записать так

I = dq/dt = (d/dt)∫σ dS = ∫(∂σ/∂t)dS = ∫(∂D/∂t)dS, (3.5)

^S ^S ^S

так как поверхностная плотность заряда σ на обкладках конденсатора равна электрическому смещению D в конденсаторе. Подынтегральное выражение в (3.5) можно рассматривать как частный случай скалярного произведения двух векторов (∂ 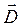/∂t) 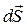, когда векторы (∂ 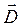/∂t) и 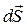взаимно параллельны. Поэтому для общего случая выражение (3.5) можно записать:

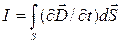Cравнивая это выражение с (3.4), имеем

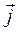_см = ∂ 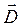/∂t.

Направление векторов плотностей токов 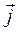и 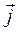_см совпадают с направлением вектора ∂ 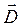/∂t.

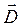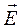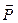В диэлектриках ток смещения состоит из двух слагаемых. Так как в диэлектрике вектор электрического смещения = ε₀ + , где 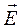– напряженность электрического поля, а 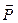– поляризованность среды, тогда плотность тока смещения будет равна

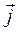_см = ε₀ ∂ 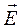/∂t + ∂ 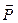/∂t, (3.6)

где ε₀∂ 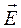/∂t – плотность тока смещения в вакууме (не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени), ∂ 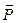/∂t – плотность тока поляризации – тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах).

Максвелл ввел понятие полного тока. Полный ток, равный сумме тока смещения и тока проводимости, всегда является замкнутым. Плотность полного тока

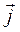_полн = 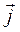+ ∂ 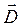/∂t. (3.7)

В зависимости от электропроводности среды и быстроты изменения электрического поля каждое из слагаемых в уравнении (3.7) дает различный вклад. В хорошо проводящих средах (металлах) и при малых скоростях изменения электрического поля ∂ 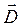/∂t плотность тока смещения пренебрежимо мала по сравнению с плотностью тока проводимости. В плохо проводящих средах (диэлектриках) и при высоких скоростях изменения ∂ 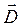/∂t ток смещения вносит основной вклад в полный ток.

Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле.

Токи смещения существуют лишь там, где меняется со временем электрическое поле, и протекают в тех участках цепи, где отсутствуют проводники, например, между обкладками заряжающегося или разряжающегося конденсатора. Токи поляризации возбуждают магнитное поле, поскольку они не отличаются от токов проводимости. Однако и другая составляющая тока смещения ( 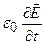), которая не связана ни с каким движением зарядов, а обусловлена только изменением электрического поля, также возбуждает магнитное поле. Даже в вакууме всякое изменение во времени электрического поля возбуждает в окружающем пространстве магнитное поле.

Открытие этого явления – наиболее существенный шаг, сделанный Максвеллом при построении теории электромагнитного поля.

Максвелл обобщил теорему о циркуляции вектора напряженности магнитного поля 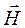,введя в нее понятие полного тока

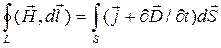–(3.8)

второе уравнение Максвелла: циркуляция вектора напряженности 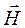магнитного поля по любому замкнутому контуру L равна суммарному току проводимости, который пронизывает поверхность S, натянутую на этот контур, сложенному со скоростью изменения потока вектора электрической индукции 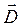через эту поверхность.

Повторяем, что переменное магнитное поле может возбуждаться движущимися зарядами(электрическими токами) и переменным электрическим полем (током смещения).

Третье и четвертое уравнения Максвелла.Теорема Гаусса для электростатического поля оказалась справедливой как для стационарного

так и для переменного электрического поля. Соответственно третье уравнение Максвелла в интегральной форме имеет вид:

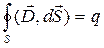, (3.9)

т.е. поток вектора 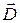электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключенных внутри этой поверхности.

Четвертое уравнение Максвелла выражает опытные данные об отсутствии магнитных зарядов (магнитное поле порождается только электрическими токами), т.е. теорема Гаусса также оказалась справедливой как для стационарного так и для переменного магнитного поля. Четвертое уравнения Максвелла в интегральной форме имеет вид:

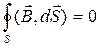, (3.10)

т.е. поток вектора магнитной индукции 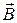сквозь произвольную замкнутую поверхность равен нулю.

Как видим, уравнения Максвелла не симметричны относительно электрического и магнитного полей, что обусловлено существованием в природе электрических зарядов и электрических токов проводимости, но отсутствием зарядов магнитных.

Интегральные уравнения Максвелла описывают среду феноменологически, не рассматривая сложного механизма взаимодействия электромагнитного поля с заряженными частицами среды.

От интегральных уравнений Максвелла (3.3), (3.8) –(3.10) можно перейти к системе дифференциальных уравнений. Четыре фундаментальных уравнения Максвелла в интегральной или дифференциальной формах не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Их необходимо дополнить соотношениями, связывающими векторы 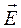, , 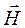, 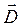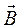и 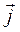, которые не являются независимыми, между ними существует следующая связь:

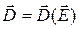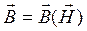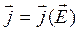, , . (3.11)

Эти уравнения называются уравнениями состояния или материальными уравнениями, они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определенную форму.

Электромагнитные свойства среды определяются уравнениями, которые в общем случае очень сложны, они могут быть интегральными, тензорными и нелинейными, однако в случае изотропной однородной проводящей неферромагнитной и несегнетоэлектрической среды имеют простой вид:

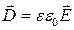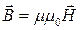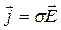, , , (3.12)

где 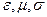− постоянные, характеризующие электрические и магнитные свойства среды (диэлектрическая и магнитная проницаемости и электропроводимость).

Уравнения (3.3), (3.8) – (3.10) и (3.12) образуют полную систему уравнений электромагнитного поля в среде, решение которой при заданных граничных условиях позволяет определить векторы 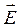, , 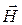, , 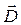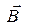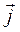и скаляр ρ (ρ -плотность распределения электрических зарядов в пространстве) в каждой точке среды с заданными ее характеристиками ε, μ, σ.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с магнитным. Электрическое и магнитное поля неразрывно связаны друг с другом, способны превращаться друг в друга и образуют единое электромагнитное поле.

Теория Максвелла не только смогла объяснить уже известные экспериментальные факты, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. Это привело Максвелла к созданию электромагнитной теории света.

Уравнения Максвелла описывают огромную область явлений. Они лежат в основе электротехники, радиотехники, связи и играют важную роль в развитии таких актуальных направлений современной физики, как физика плазмы и проблема управляемого термоядерного синтеза, магнитная гидродинамика, нелинейная оптика, астрофизика и т.д.

Уравнения Максвелла неприменимы лишь при больших частотах электромагнитных волн, когда становятся существенными квантовые эффекты, т.е. когда энергия отдельных квантов электромагнитного поля – фотонов велика и в процессах участвует небольшое число фотонов.

Контрольные вопросы:

1. Что является причиной возникновения вихревого электрического поля? Чем оно отличается от электростатического поля?

2. Чему равна циркуляция вихревого электрического поля?

3. Почему вводится понятие тока смещения? Что он собой по существу представляет?

4. Выведите и объясните выражение для плотности тока смещения.

5. В каком смысле можно сравнивать ток смещения и ток проводимости?

6.Запишите, объяснив физический смысл, обобщенную теорему о циркуляции вектора напряженности магнитного поля.

7. Запишите полную систему уравнений Максвелла в интегральной форме и объясните их физический смысл.

8. Почему постоянные электрические и магнитные поля можно рассматривать обособленно друг от друга? Запишите для них уравнения Максвелла в интегральной форме.

9. Почему уравнения Максвелла в интегральной форме являются более общими?

10. Какие основные выводы можно сделать на основе теории Максвелла?

<8 9 101112 13 14 >

Дата добавления: 2017-10-04; просмотров: 4127;