Вопрос 3. Вынужденные электромагнитные колебания. Дифференциальное уравнение вынужденных колебаний и его решение.
Для получения незатухающих колебаний нужно непрерывно пополнять энергию контура от внешнего источника, чтобы компенсировать потери на джоулево тепло, оказывая внешнее периодически изменяющееся воздействие, например, включив последовательно с элементами контура переменную э.д.с. (ε = ε0cosωt)или, разорвав контур, подавать на образовавшиеся контакты переменное напряжение (U = Umcosωt) (рис. 2.5).
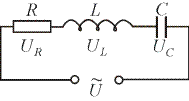
Рис. 2.5
Колебания, возникающие в CLR-цепочке при наличии переменной э.д.с., называются вынужденными.
Эту э.д.с. нужно прибавить к э.д.с. самоиндукции, в результате уравнение (2.3) примет вид
Ld2q/dt2 +Rdq/dt + q/C = Umcosωt (2.20)
– дифференциальное уравнение вынужденных гармонических колебаний.
Как известно, общее решение этого уравнения состоит из двух решений:
общего решения однородного дифференциального уравнения вида (2.9) и
частного решения неоднородного дифференциального уравнения (2.20).
Первое слагаемое быстро затухает, его время релаксации τ = 1/β. Поэтому при 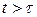 вклад в решение (2.20) дает только частное решение (второе слагаемое). Поэтому вынужденные колебания электрического заряда в цепи контура определяются частным решением этого неоднородного уравнения. Это частное решение имеет вид
вклад в решение (2.20) дает только частное решение (второе слагаемое). Поэтому вынужденные колебания электрического заряда в цепи контура определяются частным решением этого неоднородного уравнения. Это частное решение имеет вид
q = qmcos(ωt - ψ). (2.21)
Установившиеся вынужденные колебания описываются функцией (2.21), где ψ – сдвиг фаз между внешней э.д.с. и напряжением (зарядом) на конденсаторе, а
tg ψ = R/(1/ωC – ωL).
Продифференцировав выражение (2.21) по переменной t, получим выражение для силы тока в контуре при установившихся колебаниях
I = - ωqm sin(ωt - ψ) = Im cos(ωt - ψ + π/2),
где амплитуда силы тока в контуре
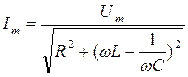 ,
,
RL = ωL – реактивное индуктивное сопротивление,
RC = 1/ωC – реактивное емкостное сопротивление,
Х=ωL – 1/ωC – реактивное сопротивление,
Z= 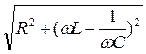
– полное (эффективное) сопротивление электрической цепи (колебательного контура).
Амплитуда вынужденных колебаний зависит не только от амплитуды внешней э.д.с., но и от ее частоты ω.
Выражение для силы тока можно записать также в виде
I = Im cos(ωt - φ), (2.22)
где φ = ψ – π/2 –сдвиг по фазе между током в контуре и приложенным напряжением, а
tgφ = tg(ψ – π/2) = –1/tgψ = (ωL –1/ωC)/R. (2.23)
Разделив выражение (2.21) на емкость, получим напряжение на конденсаторе
UC = (qm/C) cos(ωt - ψ) = UCmcos(ωt – φ –π/2), (2.24)
где
UCm = qm/C = Um/ωC 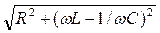 = Im/ωC. (2.25)
= Im/ωC. (2.25)
Умножив производную функции (2.22) на индуктивность L, получим напряжение на индуктивности
UL = L(dI/dt) = – ωLImsin(ωt – φ) = ULmcos(ωt – φ + π/2), (2.26)
где ULm = ωLIm.
Выражение (2. 20) можно представить в виде
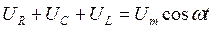 , (2.27)
, (2.27)
где 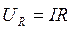 ,
, 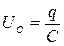 ,
, 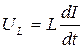 – соответственно напряжения на активном сопротивлении R, на конденсаторе С и на индуктивности L. Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени внешнему напряжению (рис. 2.5).
– соответственно напряжения на активном сопротивлении R, на конденсаторе С и на индуктивности L. Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени внешнему напряжению (рис. 2.5).
Сравнивая (2.22), (2.24) и (2.26) видим, что напряжение на конденсаторе отстает по фазе от силы тока в контуре на π/2, а напряжение на катушке индуктивности опережает ток на π/2. Напряжение на активном сопротивлении изменяется в фазе с током. Эти же результаты можно получить с помощью векторной диаграммы, как для переменных токов (рис. 2.6). Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание переменного электрического тока с частотой ω в цепи, содержащей L, C и R.
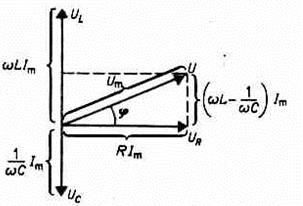
Рис. 2.6
Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колеблющейся величины, а направление вектора образует с некоторой осью угол, равный начальной фазе колебания. В качестве таковой возьмем ось токов. Тогда получится диаграмма, приведенная на рис. 2.6. Согласно (2. 27) величины где 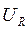 ,
, 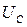 и
и 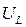 в сумме должны быть равны приложенному напряжению U. В соответствии с этим напряжение U на рис. 2.6 изображается вектором, равным сумме векторов
в сумме должны быть равны приложенному напряжению U. В соответствии с этим напряжение U на рис. 2.6 изображается вектором, равным сумме векторов 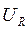 ,
, 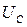 и
и 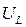 .
.
Дата добавления: 2017-10-04; просмотров: 3514;











