Вопрос 2. Плоская электромагнитная волна. Волновое уравнение для электромагнитного поля.

На расстоянии r >> λ от электрического диполя или вибратора (волновая зона) электрическое и магнитное поля изменяются в фазе по гармоническому закону и представляют собой сферическую электромагнитную волну, распространяющуюся с фазовой скоростью

,

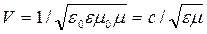где 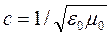– скорость света в вакууме, ε и μ – диэлектрическая и магнитная проницаемость среды. Так как εμ >1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме. При наличии дисперсии среды (зависимости скорости распространения электромагнитных волн от их частоты) скорость переноса энергии, характеризуемая групповой скоростью V_гр, может отличаться от V. В анизотропных средах V зависит также от направления распространения волны.

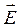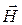С дальнейшим увеличением расстояния от вибратора радиус кривизны фронта сферической волны увеличивается, и ее можно считать плоской. Можно показать, что для однородной незаряженной непроводящей (плотность тока j=0) несегнетоэлектрической (ε = const) и неферромагнитной среды (μ = const) из уравнений Максвелла следует, что векторы напряженности и переменного электромагнитного поля удовлетворяют волновому уравнению:

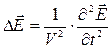, (4.1)

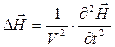, (4.2)

где 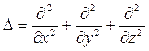– оператор Лапласа.

Следствием теории Максвелла является поперечность электромагнитных волн:векторы 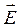и 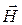напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 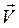скорости распространения волны, причем векторы 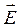, 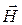и 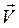образуют правовинтовую систему (рис 4.2).

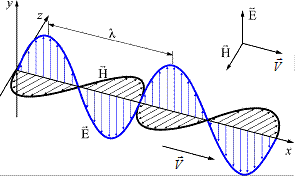
Рис 4.2

Уравнениям (4.1) и (4.2) удовлетворяют плоские монохроматические электромагнитные волны, описываемые уравнениями

Е_y = E₀cos(ωt – kx + φ), (4.3)

H_z = H₀cos(ωt – kx + φ), (4.4)

где k = ω/V – волновое число.

Векторы 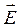и 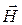всегда колеблются в одинаковых фазах, поэтому в уравнениях (4.3) и (4.4) начальные фазы φ колебаний в точках с координатой х = 0 одинаковы.

Между амплитудными Е₀ и Н₀ и мгновенными значениями Е и Н в плоской электромагнитной волне существует взаимосвязь:

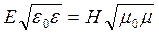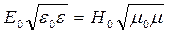; . (4.5)