Вопрос 3. Энергия электромагнитных волн.

Электромагнитные волны переносят энергию. В изотропной среде, не обладающей ферромагнитными и сегнетоэлектрическими свойствами, объемная плотность энергии электромагнитного поля w₀ складывается из объемных плотностей w_эл и w_м электрического и магнитных полей:

w₀ = w_эл + w_м = ε₀εE²/2 + μ₀μH²/2. (4.6)

Усредненные по времени плотности энергии электрического и магнитного полей одинаковы, т.е. w_эл = w_м. Поэтому можно написать, что

w₀= w_эл + w_м = ε₀εE² = 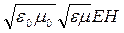. (4.7)

Полную энергию электромагнитного поля W можно определить, вычислив интеграл по объему V_об, в котором характеристики электрического и магнитного полей отличны от нуля

.

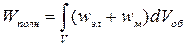Умножив плотность энергии w₀ на скорость V распространения волны в среде, получим модуль вектора плотности потока энергии S, равный энергии, переносимой электромагнитной волной в единицу времени через единичную площадку, перпендикулярную направлению переноса:

S = w₀V = EH. (4.8)

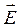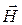Так как векторы и взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора 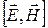совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Следовательно, вектор плотности потока электромагнитной энергии 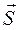(вектор Умова-Пойтинга) можно представить как векторное произведение векторов 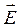и :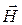

.

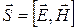Поток Ф энергии, переносимой электромагнитной волной через некоторую поверхность F, можно найти с помощью интегрирования:

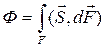.(4.9)

При распространении электромагнитной волны в средах с диссипацией энергии волна затухает, а ее энергия поглощается или рассеивается средой.