Топологические матрицы графов
Для математического описания способа соединения ветвей цепи используются матрицы соединений, контуров и сечений – прямоугольные матрицы, столбцы которых отвечают ветвям цепи, а строки – узлам, контурам и сечениям соответственно. Следовательно, различают узловые матрицы, матрицы сечений и матрицы контуров.
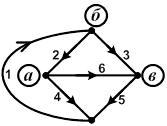
| Рассмотрим граф и составим для него матрицу [А], показывающую, к какому узлу направленного графа присоединены соответствующие ветви. Число строк в такой матрице равно количеству ветвей дерева графа, т.е. числу узлов без единицы. (Если ветвь направлена к узлу, то −1, если из узла +1, если не подходит к узлу, то 0). |
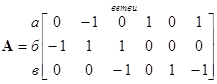
A называется матрицей соединений или узловой матрицей.
Размер матрицы  .
.
Система уравнений первого закона Кирхгофа при этом может быть записана в матричной форме:
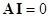 .(I – вектор-столбец токов в ветвях).
.(I – вектор-столбец токов в ветвях).
Матрица сечений Q дает информацию о принадлежности ветвей цепи к определенным сечениям. Если эта матрица составляется для главных сечений, то ее называют матрицей главных сечений. Размер матрицы  .
.
Если ветвь содержится в сечении и направлена согласно с направлением главного сечения, то соответствующий элемент матрицы имеет значение +1, если направлен иначе, то −1, если ветвь не входит в сечение, то 0.
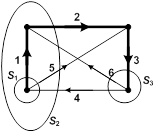
| Рассмотрим пример графа. Выделим одно из деревьев графа. Предположим, что оно образовано ветвями 1-2-3. Для данного дерева можно построить 3 главных сечения: 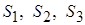 . Составим матрицу, в которой столбцами являются ветви, а строками - сечения, т.е. . Составим матрицу, в которой столбцами являются ветви, а строками - сечения, т.е.
|
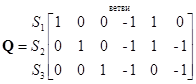 .
.
Матрицу главных сечений можно использовать для записи первого закона Кирхгофа: 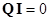 .
.
Матрица контуров В содержит информацию о том, в какие контуры цепи входят ветви. Первоочередной интерес представляют матрицы главных контуров. Напомню, что главными контурами называют контуры, в каждый из которых входит только по одной ветви связи. Направление контура определяется по направлению ветви связи, входящей в него.
В результате строки В-матрицы соответствуют главным контурам цепи, а столбцы – ветвям. Размер матрицы контуров 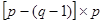 .
.
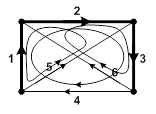
| Для анализируемого дерева графа – 3 главных контура: - образованный ветвями 1-2-3-4; - образованный ветвями 1-2-5; - образованный ветвями 2-3-6. |
В результате матрица принимает вид:
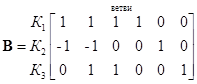 .
.
Второй закон Кирхгофа в матричной форме может быть записан как: 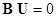 , где U – вектор-столбец, составленный из напряжений ветвей.
, где U – вектор-столбец, составленный из напряжений ветвей.
Между топологическими матрицами существует связь:
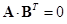 и
и 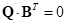 .
.
Дата добавления: 2019-12-09; просмотров: 632;











