Виды графов: тривиальные и полные графы, двудольные графы, орграфы и сети.

Определение 10.7. Граф, состоящий из одной вершины называется тривиальным.

Определение 10.8. Граф у которого любая пара вершин смежные называется полным графом.

Полный граф с Р вершинами обозначается k_p. Его максимальное количество ребер находится по формуле .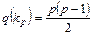

Пример.

.

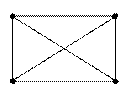
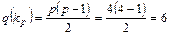Действительно, можно заметить, что данный граф имеет 6 ребер.

Определение 10.9. Полный подграф некоторого графа называется кликой этого графа.

Граф, состоящий из простого цикла с k вершинами обозначается с_k.

Определение 10.10. Двудольным графом (биграфом, чётным графом) называется такой граф G(V,E), что 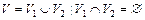, при чём всякое ребро из множества Е инцидентно вершине из V₁ и вершине из V₂. Множество из V₁ и V₂ называется долями этого графа

Определение 10.11. Если двудольный граф содержит все ребра, соединяющие множества V₁ и V₂, то такой граф называют полным двудольным графом.

Теорема. Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Определение 10.11. Если в графе ориентировать все ребра, то получится направленный орграф.

Определение 10.12. Если в графе полустепень захода некоторой вершины равна 0 (d⁺=0), то такая вершина называется источником.

Определение 10.13. Если в графе полустепень исхода некоторой вершины равна 0 (d^-=0), то такая вершина называется стоком.

Определение 10.13. Направленный граф с одним истоком и одним стоком называется сетью.