Расчет электрических цепей, основанный на применении уравнений Кирхгофа

Обычно заданными являются величины и направления всех ЭДС источников напряжения и внутренних токов источников тока и зна­чения всех внутренних и внешних сопротивлений или проводимостей цепи, а определяют токи и по ним – напряжения ветвей. Поэтому число неизвестных равно числу р ветвей схемы и, следовательно, столько же независимых уравнений нужно составить по первому и второму законам Кирхгофа,

Так как при составлении уравнений необходимо учесть направле­ния всех токов, то направлениями токов следует задаться. Применяя первый закон, токи, приходящие к узлу и уходящие от него, следует брать с разными знаками. Применяя второй закон, ЭДС и токи, направления которых совпадают с произвольно выбранным направлением обхода контура, следует считать имеющими положительный знак, остальные – отри­цательный.

Уравнения, составленные по первому закону Кирхгофа для цепи с q узлами, будут независимыми лишь для 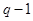узлов, так как урав­нение для последнего узла является следствием предыдущих. Следовательно, по второму закону Кирхгофа надо составить 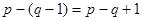независимых уравнений. Если в цепи присутствуют ветви с источниками тока, количество уравнению по второму закону Кирхгофа 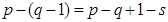, где s – количество ветвей, содержащих источники тока.

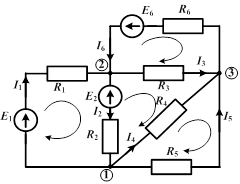
Пример составления системы уравнений.

Изображенная на рисунке цепь имеет 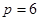ветвей, 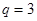узла и 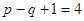элементарных контура.

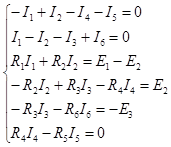
Решая систему уравнений любым известным из алгебры способом, находят все неизвестные токи ветвей. Отрицательный знак указывает на то, что действительное направление тока обратно выбранному направлению.

Достоинством рассмотренного метода является его общность, а недостатком – громоздкость решения системы, состоящей из боль­шого числа уравнений. Поэтому кроме непосредственного использо­вания уравнений по законам Кирхгофа применяются специальные методы расчета сложных цепей: либо упрощающие их схемы (методы наложения и эквивалентного источника энергии), либо уменьшающие число неизвестных (методы контурных токов и узловых напряжений).