Вычисление ранга матрицы методом элементарных преобразований.
Элементарными преобразованиями матрицы являются:
1. транспонирование,
2. умножение всех элементов строки (или столбца) на число 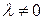 ,
,
3. перестановка строк (или столбцов),
4. прибавление к элементам строки (или столбца) соответствующих элементов другой строки (или другого столбца), умноженных на число 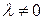 ,
,
5. вычеркивание строк (столбцов), состоящих из нулей.
Теорема 1. Элементарные преобразования не меняют ранга матрицы.
(без доказательства)
Определение 4. Матрицы А и В называются эквивалентными, если их ранги равны А ~ В 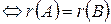 .
.
Элементарные преобразования можно проводить по схеме Гаусса:
1. сделать 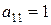 ,
,
2. обнулить первый столбец, кроме 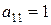 , вычитая из всех нижележащих строк первую, умноженную на первый элемент соответствующей строки
, вычитая из всех нижележащих строк первую, умноженную на первый элемент соответствующей строки 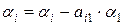 ,
,
3. сделать 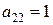 ,
,
4. обнулить второй столбец, кроме 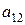 и
и 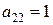 , вычитая из всех нижележащих строк вторую, умноженную на первый элемент соответствующей строки
, вычитая из всех нижележащих строк вторую, умноженную на первый элемент соответствующей строки 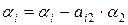 ,
,
5. и т.д.
Таким образом можно любую матрицу привести к треугольному виду, а отсюда следует, что ранг матрицы равен числу ненулевых элементов, стоящих на главной диагонали.
Пример.
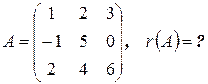 .
.
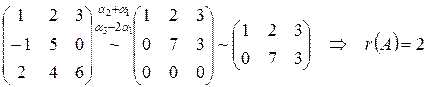 , т.к. минор второго порядка
, т.к. минор второго порядка 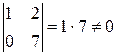 .
.
Обратная матрица.
Определение 5. Квадратная матрица п – го порядка называется невырожденной, если ее определитель не равен нулю.
Пример.
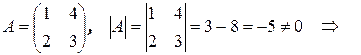 матрица А – невырожденная.
матрица А – невырожденная.
Определение 6. Квадратная матрица 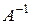 называется обратной к матрице А, если выполняется условие
называется обратной к матрице А, если выполняется условие 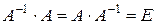 .
.
Пример.
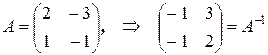 , т.к.
, т.к. 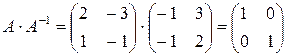 и
и 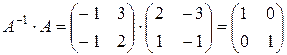 .
.
Свойства обращения матриц.
1°. 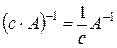 ;
;
2°. 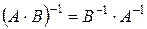 ;
;
3°. 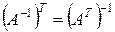 ;
;
4°. 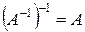 .
.
Дата добавления: 2020-03-17; просмотров: 816;











