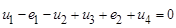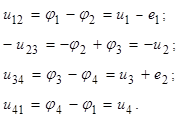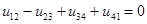Основные задачи теории электрических цепей
При исследовании электрических цепей выделяют две основные задачи – анализа и синтеза.
Задача анализа – заданы воздействия, структура цепи и параметры элементов; требуется определить реакцию цепи.
Задача синтеза – заданы воздействия и реакции цепи; требуется определить структуру и параметры элементов цепи.
Напряжения источников ЭДС и токи источников тока называются воздействиями. Все остальные токи и напряжения называются реакциями цепи.
Свойства линейных электрических цепей
Линейные электрические цепи – цепи, состоящие только из линейных элементов. Линейные элементы те, параметры которых не зависят от величины токов и напряжений (от величины электромагнитного поля).
Линейные электрические цепи удовлетворяют принципу суперпозиции (наложения), согласно которому реакция цепи на совокупность воздействий равна сумме реакций, вызываемых в этой цепи каждым воздействием в отдельности.
Графическое изображение электрической цепи называется электрической схемой.
|
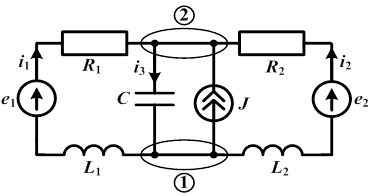
В общем случае электрическая цепь и, следовательно, схема, состоит из ветвей и узлов.
Ветвь – это участок электрической цепи (схемы), вдоль которого протекает один и тот же ток. Элементы ветви соединены последовательно, а общее напряжение равно алгебраической сумме напряжений на каждом элементе. Направление напряжения учитывается знаком слагаемого.
Параллельное соединение нескольких ветвей означает, что они подсоединены к одной и той же паре узлов, и к ним приложено одно и то же напряжение.
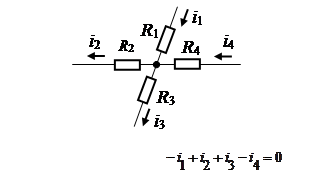
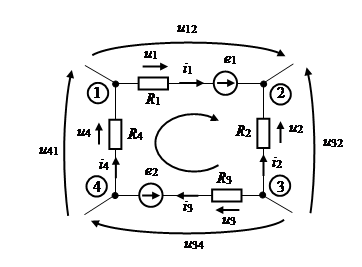
На рисунке приведена электрическая цепь, четыре ветви которой соединены параллельно.
Узел (вершина) – место соединения трех и более ветвей электрической схемы.
Основные законы электрических цепей
Для расчета электрических цепей необходимо учитывать направление токов и напряжений. Хотя в общем случае ток является движением электрических зарядов разных знаков в противоположные стороны, условным положительным направлением тока принято считать направление перемещения положительных зарядов, т. е. от положительного зажима источника к отрицательному “-“.Если ток идет в противоположном направлении, он получает отрицательный знак.
В соответствии с законом Ома положительное направление напряжения совпадает с положительным направлением тока. Если направление тока неизвестно, его приходится выбирать произвольно и определять направление в результате расчета по знаку тока (напряжения).
Основные уравнения цепей вытекают из уравнений Максвелла, в частности из принципа непрерывности электрического тока и закона электромагнитной индукции.
Из принципа непрерывности получаем первый закон Кирхгофа:
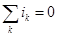 ,
,
алгебраическая сумма токов в ветвях, образующих узел, равна
нулю. При этом токи, уходящие от узла считают положительными,
а токи, приходящие к узлу – отрицательными.
|
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру электрической цепи, поскольку и в данном случае накопление заряда отсутствует. Контуром называется замкнутый путь, проходящий по нескольким ветвям. В зависимости от числа контуров. Если к узлу присоединен источник тока, то ток этого источника также необходимо учитывать.
Из закона электромагнитной индукции получаем второй закон Кирхгофа в следующем виде
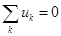 ,
,
т. е. алгебраическая сумма напряжений на ветвях, образующих контур, равна нулю. При этом со знаком «плюс» учитываются величины, совпадающие по направлению с направлением обхода контура. При этом помним, что напряжения совпадают по направлению с током. Если в ветвях контура включены источники напряжения, то формулировку можно изменить: алгебраическая сумма падений напряжения на пассивных элементах цепи равна алгебраической сумме ЭДС источников, действующих в этом контуре.
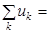
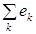 .
.
Обход контура осуществляют в произвольно выбранном направлении, (например по часовой стрелке) с соблюдением следующего правила: все контурные ЭДС и падения напряжения, совпадающие с выбранным обходом, записываются с одинаковыми знаками.
|
|
Закон Джоуля-Ленца. Мгновенная мощность p, [Вт], рассеянная в сопротивлении R при протекании электрического тока i, равна:
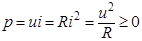 .
.
Энергия, [Вт∙с], потребляемая сопротивлением, начиная от момента времени равного нулю и до некоторого момента времени t, будет равна:
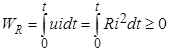 .
.
Дата добавления: 2019-12-09; просмотров: 704;