Вычисление ранга матрицы

а) Метод окаймляющих миноров.

.

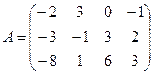Пусть в матрице найден минор 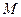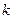-го порядка, отличный от нуля. Рассмотрим лишь те миноры 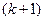-го порядка, которые содержат в себе (окаймляют) минор 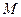: если все они равны нулю, то ранг матрицы равен 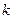. В противном случае среди окаймляющих миноров найдется ненулевой минор 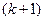-го порядка, и вся процедура повторяется.

Применяя описанный метод к матрице 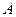, найдем .

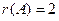Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.

б) Метод элементарных преобразований

Элементарными преобразованиями называют следующие преобразования матриц:

1) Умножение или деление строки на число, отличное от нуля;

2) Сложение и вычитание строк;

3) Перестановку строк;

4) Вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) Транспонирование

Те же операции, применяемые для столбцов, также являются элементарными преобразованиями.

Теорема. Элементарные преобразования не меняют ранга матрицы.