АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Расчет электрических цепей методом эквивалентных преобразований
Преобразование называется эквивалентным, если напряжения и токи в остальной части схемы при этом не меняются.
1. Последовательное соединение – по второму закону Кирхгофа:
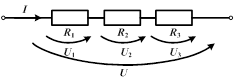
| 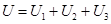 , ,
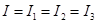 , ,
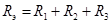 . .
|
2. Параллельное соединение – по первому закону К.
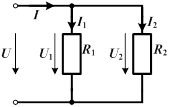
| 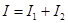 , ,
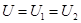 , ,
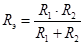 . .
|
3. Смешанное соединение
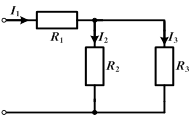
| 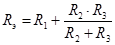 .
Формула токового делителя: .
Формула токового делителя:
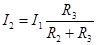 , , 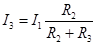 . .
|
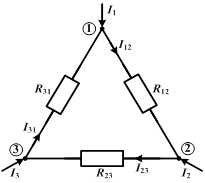
4. Преобразование из «треугольника» в «звезду» и обратно.
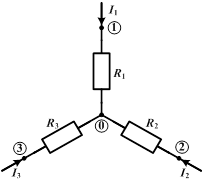
| 
|
| соединение «звездой» | соединение «треугольником» |
Формулы преобразований могут быть получены, используя законы Ома и Кирхгоффа:
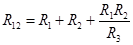 ; ;
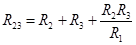 ; ;
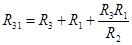 . .
| 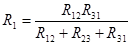 ; ;
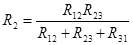 ; ;
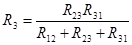 . .
|
Метод наложения
Для любых линейных систем справедлив принцип наложения (или иначе принцип суперпозиции), в соответствии с которым реакция от воздействия нескольких сил равна сумме реакций от каждого воздействия в отдельности.
Если рассмотреть принцип суперпозиции применительно к теории линейных электрических цепей, его можно перефразировать следующим образом:
Ток каждой ветви сложной цепи с несколькими источниками напряжения или тока равен алгебраической сумме токов этой ветви, протекающих под действием каждого источника в отдельности.
Если для узлов и контуров любой электрической цепи, содержащей источники напряжения с ЭДС 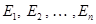 написать уравнения по законам Кирхгофа, получается система линейных уравнений, вида
написать уравнения по законам Кирхгофа, получается система линейных уравнений, вида
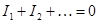 ,
, 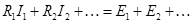 ,
,
из которой ток каждой ветви определяется однозначно.
Если поочередно предположить, что в цепи существует только ЭДС 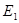 а остальные равны нулю, затем – только ЭДС
а остальные равны нулю, затем – только ЭДС 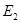 и т. д., можно для каждой ЭДС вычислить соответствующие ей токи ветвей, составив уравнения по законам Кирхгофа при тех же направлениях ЭДС и токов:
и т. д., можно для каждой ЭДС вычислить соответствующие ей токи ветвей, составив уравнения по законам Кирхгофа при тех же направлениях ЭДС и токов:
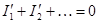 ,
, 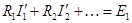 ,
,
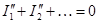 ,
, 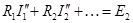 ,
,
и т.д.
Сложение почленно этих уравнений
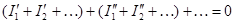 ,
,
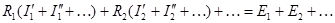 ,
,
даст систему, которая также имеет единственное решение для всех неизвестных 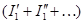 ,
, 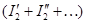 и т. д. Из сравнения исходных и только что полученных уравнений, имеющих одинаковые коэффициенты и правые части, видно, что решения обеих систем должны совпадать, следовательно,
и т. д. Из сравнения исходных и только что полученных уравнений, имеющих одинаковые коэффициенты и правые части, видно, что решения обеих систем должны совпадать, следовательно,
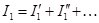 ,
, 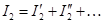 ,
,
т. е. ток каждой ветви цепи равен алгебраической сумме токов этой ветви, протекающих под действием каждой э. д. с. в отдельности.
На принципе наложения основан метод наложения. Он состоит в определении и последующем суммировании токов ветвей от каждой ЭДС в отдельности. При этом остальные ЭДС приравниваются нулю, т. е. нужно мысленно их удалить и представить замкнутыми накоротко каждую пару тех точек цепи, между которыми действуют эти ЭДС. Тогда от этих источников в цепи остаются только их внутренние сопротивления.
Напряжение на каком-либо участке цепи с сопротивлением R:
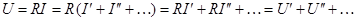 ,
,
т. е. напряжение на участке цепи ровно алгебраической сумме напряжений для каждой составляющей тока. Следовательно, и при определении напряжений может быть применен метод наложения.
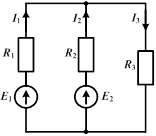
Метод наложения целесообразно применять в том случае, если, приравнивая нулю все ЭДС, кроме одной, можно упростить цепь.
| 
| 
|
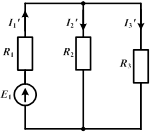
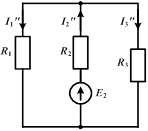
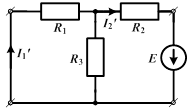
Например, для изображенной цепи при 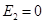 или
или 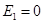 получаются, соответственно, параллельно-последовательные цепи, легко рассчитываемые методом преобразования.
получаются, соответственно, параллельно-последовательные цепи, легко рассчитываемые методом преобразования.
При этом действительное направление составляющих токов определяется направлением ЭДС и, выбирая произвольно направления результирующих токов, при наложении следует совпадающие с ними по знаку составляющие брать положительными, и наоборот. Так, для направлений токов, указанных на рисунке
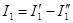 ,
, 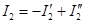 и
и 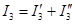
Принцип наложения основан на линейном характере уравнений по законам Ома и Кирхгофа при постоянстве коэффициентов уравнений, т. е. сопротивлений цепи.
Если метод наложения применять в случае, когда источниками энергии являются источники тока и считать несуществующим источник в какой-либо ветви, т. е. принимать его внутренний ток J = 0, следует представить себе цепь этого тока разомкнутой;тогда от источника тока в цепи остается только его внутренняя проводимость GB.
Необходимо отметить, что наложение неприменимо для мощностей, так как они являются квадратичными функциями токов и напряжений.
Принцип взаимности
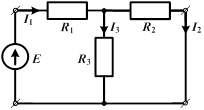
| Пусть в первую ветвь Т-образной схемы, состоящей из трех разных сопротивлений 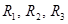 соединенных звездой,включена ЭДС Е, а выходные зажимы замкнуты. Направление токов всех ветвей определяется направлением ЭДС E. соединенных звездой,включена ЭДС Е, а выходные зажимы замкнуты. Направление токов всех ветвей определяется направлением ЭДС E.
|
Ток 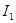 распределится между параллельно соединенными второй и третьей ветвями обратно пропорционально их сопротивлениям. Тогда ток во второй ветви
распределится между параллельно соединенными второй и третьей ветвями обратно пропорционально их сопротивлениям. Тогда ток во второй ветви
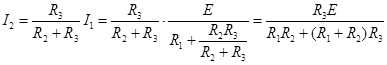 .
.
Если поменять местами индексы 1 и 2,очевидно, получится значение тока 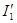 в первой ветви при таком переносе ЭДС Е во вторую ветвь, чтобы ее направление совпало с направлением тока в первой ветви при таком переносе ЭДС Е во вторую ветвь, чтобы ее направление совпало с направлением тока 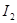 . Выражение . Выражение 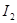 симметрично относительно этих индексов, поэтому симметрично относительно этих индексов, поэтому 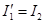 . .
| 
|
Установленный принцип взаимности для Т-образной схемы имеет самый общий характер и может быть сформулирован следующим образом:
если ЭДС Е, действуя в любой ветви сколь угодно сложной цепи, не содержащей других ЭДС, вызывает в другой ветви ток I, то перенесенная в нее та же ЭДС вызовет в первой ветви такой же ток I.
Принцип взаимности был установлен Кирхгофом.
На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одной ЭДС, когда ее перенос упрощает цепь.
Дата добавления: 2019-12-09; просмотров: 718;











