Понятие аналитического сигнала

Представление детерминированных сигналов рядами ортогональных функций полезно при анализе прохождения сигналов через линейные радиотехнические устройства.

При анализе нелинейных преобразований сигналов и, в частности, модуляции и демодуляции, требуется иной подход. Этот подход основывается на понятии аналитического сигнала.

Многие формулы гармонического анализа записываются значительно проще и некоторые задачи решаются легче, если использовать в качестве элементарных функций экспоненциальные функции мнимого аргумента, например комплексная огибающая легко отделяется от множителя с несущей частотой при выражении сигнала в комплексной форме.

A∙cos[j(ω₀t + φ)] = [А∙ехр(j φ)]∙ехр(ω₀t).

Если разложить косинус суммы по формуле Эйлера [6, 21], то:

cos(ωt + φ) = 1/2[exp{j(ωt + φ)} + exp{-j(ωt + φ)}]. (6.1)

Этой записи можно дать геометрическую трактовку, пользуясь представлением комплексных чисел в виде точек или векторов на плоскости.

Выражение exp{j(ωt + φ)} представляет в данном случае вектор единичной длины, проведенный под углом ωt + φ к действительной оси (рис. 6.1). При изменении времени t этот вектор единичной длины меняет положение, вращаясь в положительном направлении с угловой скоростью ω.

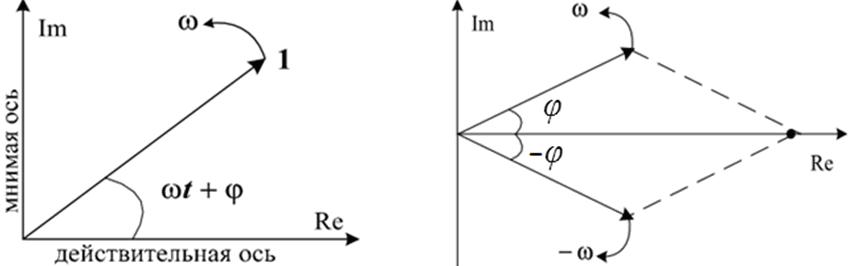
Рис. 6.1. Геометрическая трактовка Рис. 6.2. Экспоненциальное

трактовка экспоненциальной ф-ции представление элементарной

мнимого аргумента функции

Изобразить синусоиду в форме (6.1), это значит представить ее суммой двух векторов, длина каждого из которых равна 1/2, расположенных в любой момент времени симметрично относительно действительной оси и вращающихся в разных направлениях с угловыми скоростями ω и -ω (рис. 6.2).

В момент t = 0 они занимают положения под углами φ и –φ относительно действительной оси. Геометрическая сумма векторов всегда совпадает по направлению с действительной осью и представляет действительную функцию времени cos(ωt + φ).

При представлении косинусоиды в виде cos(ωt + φ) = Re[exp{j(ωt + φ)}] можно ограничиться одним вращающимся в положительном направлении вектором и представить косинусоиду его проекцией на действительную ось.

В этом случае нет необходимости вводить отрицательные частоты. Длина вектора представляет амплитуду косинусоиды, а угол, образуемый им в данный момент с действительной осью – полную фазу (ωt + φ).

Проекция этого вектора на мнимую ось равна Im[exp{j(ωt + φ)}] = sin (ωt + φ), т.е. представляет ту же косинусоиду, сдвинутую по фазе на π/2 (рис. 6.3).

Значительное количество сигналов применяемых в системах электросвязи можно представлять в виде:

s(t) = A(t)∙cos[ωt + φ(t)], (6.2)

т.е. как «квазигармоническую» функцию с переменными «амплитудой» и «начальной фазой».

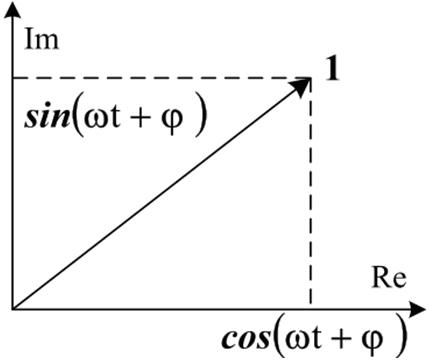
Рис. 6.3. Проекции единичного вектора на действительную и мнимую оси

Такой сигнал можно интерпретировать геометрически как проекцию на действительную ось вращающегося вектора, но при этом изменяющего свою длину и угловую скорость. Для описания свойств сигнала представленного в форме (6.2) вводят понятие комплексного аналитического сигнала.

Аналитический сигнал формируется путем отбрасывания области отрицательных частот спектра вещественного сигнала и удвоения спектра в области положительных частот. Так, если s(t) – вещественный сигнал, записываем s(t) ↔ S(f) и аналитический сигнал

s_a(t) ↔ 2σ(f)∙X(f), (6.3)

где σ(f) – единичная ступенчатая функция в частотной области.

Единичная ступенчатая функция равна нулю в интервале от минус бесконечности до некоторой точки и единице в интервале от этой точки до плюс бесконечности. Ступенчатая функция во временной области имеет вид

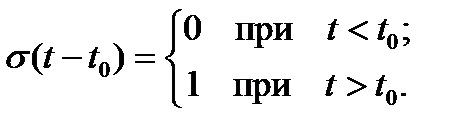(6.4)

Преобразование Фурье единичной ступенчатой функции равно

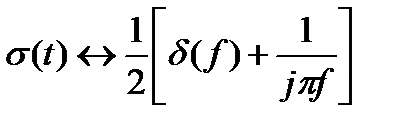. (6.5)

Таким образом, можно определить единичную ступенчатую функцию в частотной области и ее преобразование Фурье. Пусть

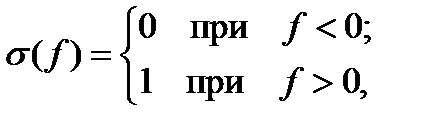
тогда

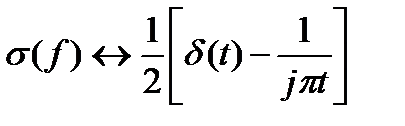. (6.6)

Заметим, что если s(t) – синусоида постоянной амплитуды, то операция, указанная в выражении (6.3), состоит просто в замене вещественной синусоиды комплексной экспонентой. В более общем случае для нахождения вещественной и мнимой частей s_a(t) можно преобразовать спектр в выражении (6.3) во временную область:

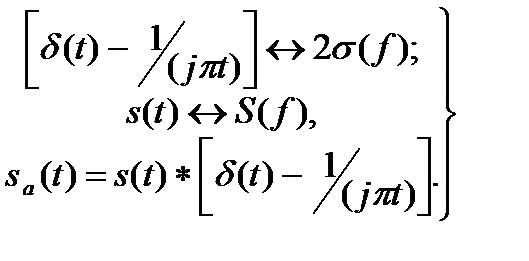(6.7)

Свертка s(t) с импульсной функцией не меняет s(t), поэтому можно записать

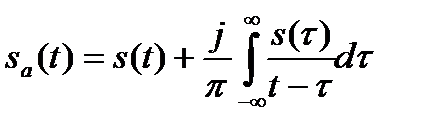(6.8)

Вещественная часть s_a(t) является исходной вещественной функцией, а мнимая часть определяется в формуле (6.8) интегралом от функции, содержащей s(t). Этот интеграл называется преобразованием Гильберта функции s(t) и обозначается

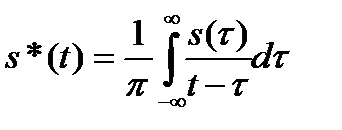.(6.9)

Существует следующее обратное соотношение:

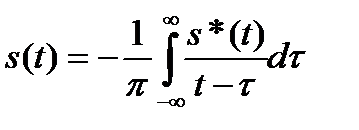. (6.10)

Таким образом, s(t) и s*(t) представляют собой пару преобразований Гильберта и аналитический сигнал можно записать как

s_a(t) = s(t) + js*(t). (6.11)

Исходя из этого, аналитический сигнал в момент времени t может быть представлен точкой на комплексной плоскости, если по оси абсцисс откладывать значения реального сигнала s(t), а по оси ординат – сопряженного с ним сигнала s*(t), (рис. 6.4).

Легко показать, что функция sin(ω₀t)является преобразованием Гильберта cos(ω₀t). Поэтому аналитический сигнал, соответствующий cos(ω₀t), имеет вид s_а(t) = cos ω₀t + j sin ω₀t = =exp(jω₀t). Аналитический сигнал общего вида удобно представлять в экспоненциальной форме как

s_a(t) = |s_a(t)|exp [jФ(t)], (6.12)

где |s_a(t)| = [s²(t) + j∙s*²(t)]^1/2;

Ф(t) = arctg [s*(t)/s(t)].

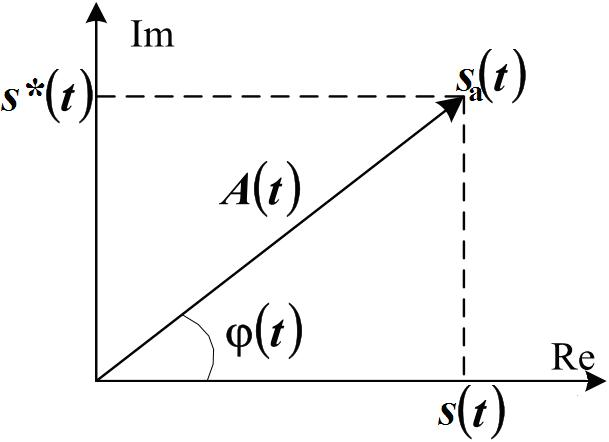
Рис. 6.4. Представление аналитического сигнала точкой

Теперь положим Ф(t) = ω₀t + φ(t) и запишем

s_a(t) = |s_a(t)| ехр [jφ(t)] ехр (jω₀t) = m(t) exp (jω₀t). (6.13)

Комплексная огибающая m(t) получается удалением комплексного множителя, связанного с несущей, из аналитического сигнала:

m(t) = s_a(t)∙ехр (-jω₀t) = |s_a(t)| ехр [jφ(t)]. (6.14)

Если m(t) – узкополосная относительно f₀ функция, то она будет обладать свойствами, которые мы интуитивно связываем с огибающей. В противном случае это просто удобное математическое представление.

Для получения спектра функции s*(t) можно применить функцию sign, которая тесно связанной с единичной ступенчатой функцией и определяется как

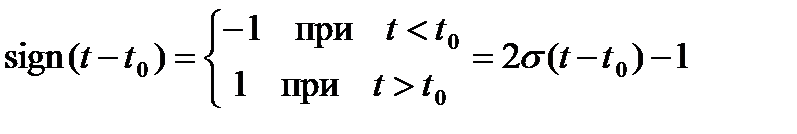. (6.15)

Соотношение между функцией sign и единичной ступенчатой функцией σ(t) показано графически на рис. 6.5.

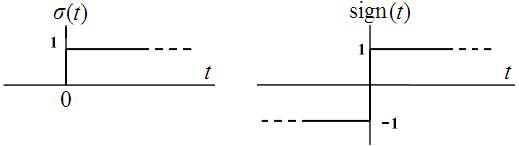
Рис. 6.5. Единичная ступенчатая функция σ(t) и функция sign (t)

Функция sign может быть определена и в частотной области sign (f). С помощью выражений (6.5) и (6.15) получаются следующие соотношения для пар преобразований:

Функция sign может быть определена и в частотной области sign (f). С помощью выражений (6.5) и (6.15) получаются следующие соотношения для пар преобразований:

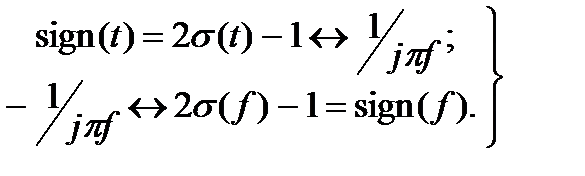. (6.16)

Таким образом, спектр функции s*(t) имеет вид:

l/πt ↔ -j∙sign (f);

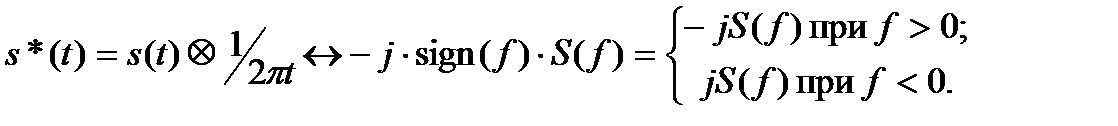(6.17)

С помощью обобщения теоремы Парсеваля можно показать, что s(t) и s*(t) ортогональны. Для двух заданных функций s₁(t) и s₂(t) обобщенное соотношение Парсеваля состоит в том, что

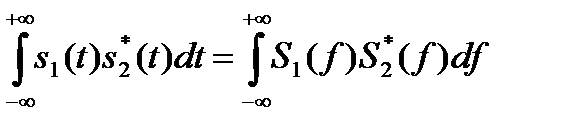(6.18)

откуда

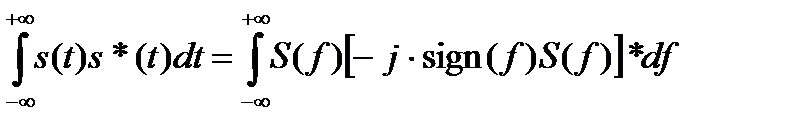, (6.19)

но S(f)[ -j∙sign (f)∙S(f)]* = j| S(f)|² ∙ sign (f).

В силу того, что эта функция частоты нечетна, интеграл в выражении (6.19) по всему частотному диапазону равен нулю. Поэтому

.

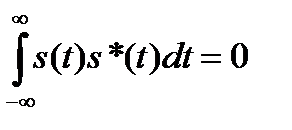Спектральные плотности энергии s(t) и s*(t) одинаковы, следовательно, полная энергия аналитического сигнала в два раза больше энергии вещественного.