Нормальный случайный процесс (гауссов процесс)

Процесс называется нормальным или гауссовым, если его одномерная ФПВ имеет вид:

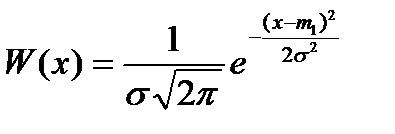
Графики нормальной ФПВ построены на рис. 5.2:

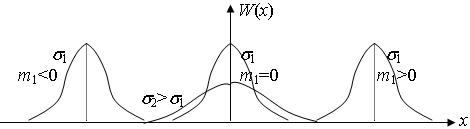
Рис. 5.2. Графики нормальной функции плотности вероятности СП:

m₁ – среднее значение случайного процесса; s² – дисперсия случайного процесса

Свойства нормального случайного процесса.

1. W(x) ³ 0

2. Нормальная ФПВ симметрична относительно x = m₁

3. W(x) – max при х = m₁

4. Площадь под кривой W(x) равна 1.

5. При изменении m₁ форма кривой не меняется, но кривая смещается вдоль оси х.

6. Чем больше дисперсия s², тем кривая ниже и шире.

7. С вероятностью близкой к 1 (Р @ 0,997) мгновенные значения нормального случайного процесса лежат в пределах: m₁ - 3s < x < m₁+3s

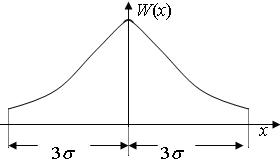
Рис. 5.3. Пределы распределения СП с вероятностью 0,997

Если известна дисперсия и m₁, то рабочий участок ВАХ должен иметь протяженность m₁ ± 3s.

ФРВ для нормального случайного процесса

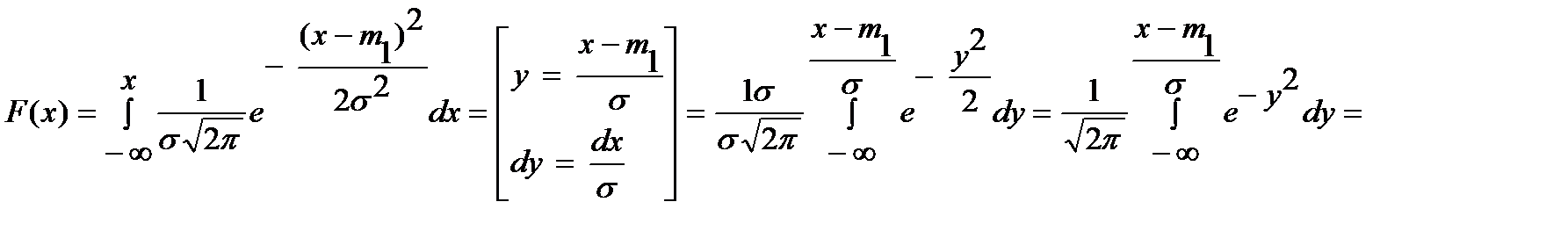
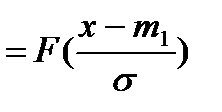– табулированная функция (интеграл вероятности Лапласа)

F(0) = 0,5 F(-x) = 1- F(x)

F(3,9) = 0,99995 F(-¥) = 0; F(¥) = 1.

ФРВ для нормального процесса имеет вид:

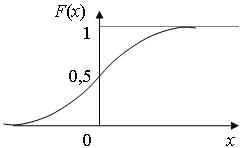
Рис. 5.4. Функция распределения вероятностей нормального процесса