Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса

Комплексный сигнал можно представить в форме [6]:

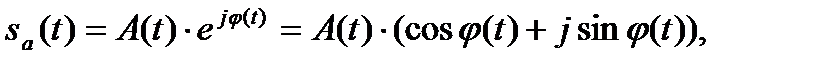(6.20)

где 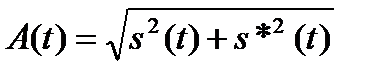называют огибающей сигнала, (6.21), а

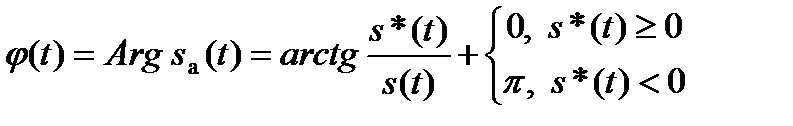мгновенной фазой сигнала.

Здесь s(t) = A(t)∙cos φ(t); s*(t) = A(t)∙ sin φ(t)

Функция φ(t) называется мгновенной фазой сигнала.

Производная от мгновенной фазы сигнала по времени называется мгновенной частотой сигнала:

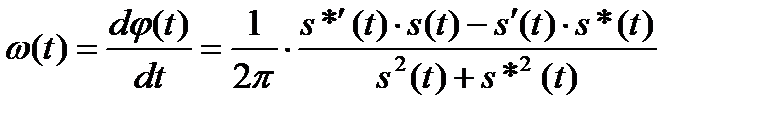. (6.22)

Например, для гармонического сигнала [6]:

.

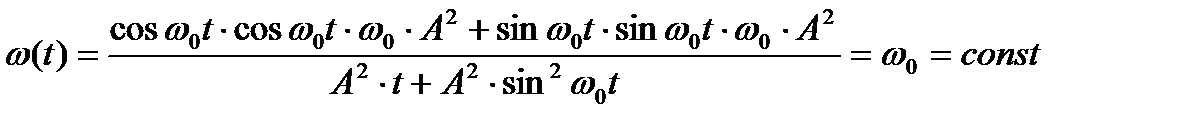В общем случае мгновенная частота изменяется во времени.

Из (6.21) следует, что A(t) ≥ s(t), причем равенство достигается в моменты времени, когда s*(t) = 0. В этих точках производная A(t) совпадает с производной сигнала s(t):

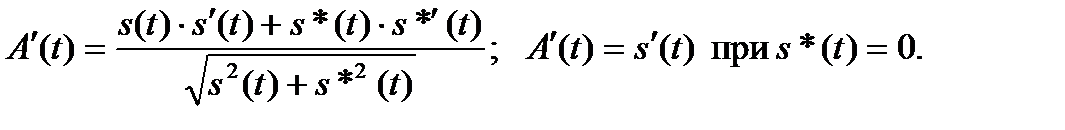(6.23)

Следовательно, при s*(t) = 0, огибающая A(t) касается сигнала s(t).

Функция cos(φ(t)) называется высокочастотным заполнением сигнала.

Процесс формирования сигнала на основе огибающей A(t) и фазы φ(t) показан на рис. 6.6.

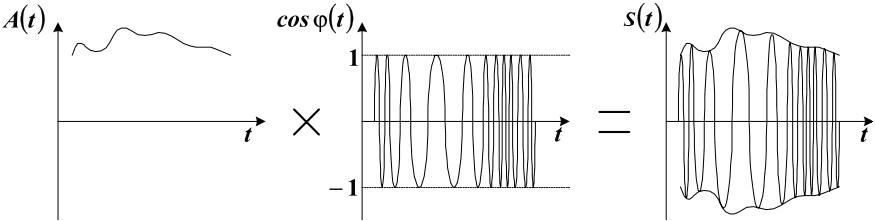
Рис. 6.6. Временное представление огибающей и высокочастотного заполнения

Если мгновенная частота колеблется вокруг среднего значения ω_ср, то можно записать:

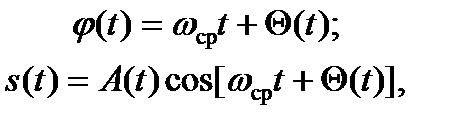(6.24)

где Θ(t) – называется мгновенной начальной фазой сигнала.

Выражение (6.24) удобно для описания узкополосных сигналов. В этом случае основная часть спектра амплитуд сосредоточена в относительно узкой, по сравнению с A(t) и φ(t), полосе частот. При этом A(t) и φ(t) изменяются медленно по сравнению с cos(ω_ср∙t). Такие сигналы называются квазигармоническими. У случайных сигналов и помех A(t), φ(t), ω(t), ω_ср(t) и Θ(t) являются случайными функциями времени.