Автокорреляция дискретного сигнала

По аналогии с формулой (7.1) АКФ дискретного сигнала {s_k} и его задержанной копии на время τ = nΔt_д {s_k-n} может быть представлена в виде

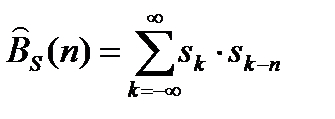. (7.6)

Эта функция, зависящая от числа тактов сдвига дискретной последовательности n, как и обычная АКФ, является четной, т. е. При нулевом сдвиге n = 0 дискретная АКФ определяет энергию дискретного сигнала

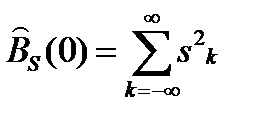. (7.7)

В качестве примера рассчитаем АКФ дискретного аналога импульса прямоугольной формы с единичными амплитудами {1, 1, 1}. Копии этого сигнала и значения дискретной АКФ имеют вид рис. 7.3:

n = 0, {1, 1, 1}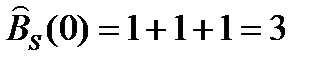

n = 1, {0, 1, 1, 1}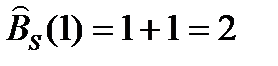

n = 2, {0, 0, 1, 1, 1}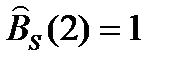

n = 3. {0, 0, 0, 1, 1, 1}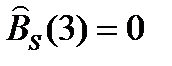

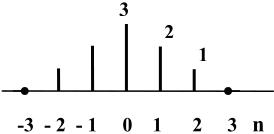
Рис. 7.3. Автокорреляционная функция дискретного сигнала

Как и в случае аналоговых видеоимпульсов, лепестки дискретной АКФ с увеличением сдвига n уменьшаются по линейному закону.

Изменим форму дискретного сигнала, так что он будет описываться в виде последовательности {1, 1, – 1}. Тогда его АКФ будет иметь вид рис. 7.4:

n = 0, {1, 1, -1}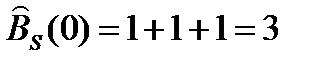

n = 1, {0, 1, 1, -1}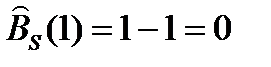

n = 2, {0, 0, 1, 1, -1}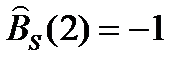

n = 3. {0, 0, 0, 1, 1, -1}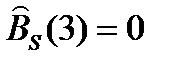

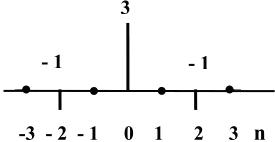
Рис. 7.4. Автокорреляционная функция дискретного сигнала

Сравнивая дискретные АКФ на рис. 7.3 и рис. 7.4, можно отметить, что именно сигнал {1, 1, – 1} имеет наиболее совершенную с точки зрения уровня боковых лепестков корреляционную функцию. Этот сигнал является простейшим из семейства сигналов Баркера, представляющих из себя М-позиционные сигналы, у которых значения боковых лепестков АКФ при n ≠ 0 не превышают единицы. Энергия этих сигналов 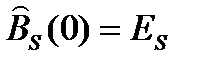всегда равна числу позиций М. Доказано, что число М в сигналах Баркера не может превышать числа 13. К настоящему времени известны сигналы, у которых число позиций M равно 3, 4, 5, 7, 11 и 13.