Возрастающим значениям интегральной кривой соответствуют положительные значения дифференциальной кривой, убывающим – отрицательные значения.

Непосредственное применение указанного способа построения графиков не практикуется из-за сложности точного построения касательных. Обычно используется его модификация, носящая название метод хорд: касательные, проведенные в точках, лежащих на серединах выбранных частков, заменяются хордами этих участков.

Выбрав полюсное расстояние h и отложив его влево от оси ординат графика дифференциальной кривой, получим полюс p ( рис. 2.13,б). Из этого полюса строятся лучи параллельные хордам участков интегральной кривой. Отрезки, отсекаемые этими лучами на оси ординат, определяют значения производных для середин соответствующих участков, так как они пропорциональны тангенсам углов наклона касательных на серединах участков. Если масштабные коэффициенты по осям графика интегральной кривой известны, можно определить масштабные коэффициенты по осям графика дифференциальной кривой. Рассмотрим, например, графики S(t) и V(t).

Очевидно, что

V = y_v k_v= ∆S k_s /∆t k_t.

Из подобия треугольников следует:

∆S/∆t = y_v / h,

откуда после подстановки в предыдущее выражение следует:

k_v = k_S / h_v k_{t .}

Аналогичным образом выводится формула:

k_a = k_v/h_a k_{t .}

2.8. Аналитический метод исследования открытой

кинематической цепи

Известно довольно много различных методов аналитического исследования кинематики рычажных механизмов. Рассмотрим один из них – метод преобразования координат.

На рис.2.14 представлена плоская открытая кинематическая цепь, составленная их трех звеньев, соединенных между собой посредством вращательных кинематических пар. Конфигурация цепи определяется обобщенными координатами φ₁, φ₂, φ₃. Пусть заданы размеры звеньев (их длины) L₁, L₂ и положение т. М на третьем звене. Требуется определить положение т.М в неподвижной системе координат XY, связанной со стойкой.

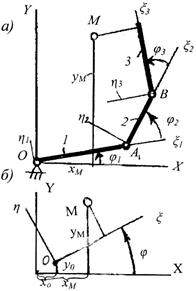
Рис. 2.14. Открытая кинематическая цепь: системы координат звеньев- а, преобразование координат на плоскости – б

Введем подвижные системы координат ξ¹η¹, ξ²η², ξ³η³, связав их со звеньями 1, 2 и 3, как указано на рис.2.14. Воспользуемся уравнениями преобразования координат, которые вытекают из простых геометрических построений на рис.2.14,б:

x_M = cosφ ξ_M – sinφ η_M + x_O;

y_M = sinφ ξ_M + cosφ η_M + y_O.

Применив уравнения преобразования координат последовательно к координатным системам ξ¹η¹, ξ²η², ξ³η³, XY, получим систему линейных уравнений. Решение этой простой системы не вызывает затруднений, тем более что здесь применяется рекуррентный метод расчета: результаты, полученные при расчете первой пары уравнений , подставляются в правую часть второй пары уравнений и т.д. При большом числе звеньев и при необходимости расчета большого числа положений механизма целесообразно расчет производить на ЭВМ.

2.9. Кинематическое исследование рычажных механизмов с замкнутыми цепями

Большинство рычажных механизмов образовано из замкнутых кинематических цепей. Аналитическое исследование таких механизмов представляет задачу, родственную рассмотренной выше. В обоих случаях используются уравнения преобразования координат. Из замкнутой кинематической цепи путем размыкания одной кинематической пары образуются две открытые кинематические цепи. Для каждой из них составляются уравнения преобразования координат. К ним добавляются уравнения, вытекающие из уравнений связей, налагаемых кинематическими парами. Таким образом, получается система уравнений, как правило нелинейная, из которой отыскиваются координаты, определяющие положение (конфигурацию) кинематической цепи.

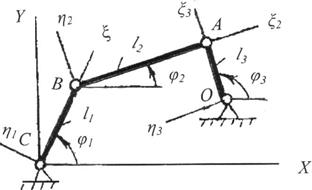
Рис. 2.15. Четырехзвенный рычажный механизм и связанные системы координат

Решаемая таким образом задача является обратной по отношению той, которая была решена для открытой цепи: по известному положению некоторой точки или входного звена находятся относительные положения остальных звеньев. Напомним, что прямая задача состояла вопределении положения точки, принадлежащей n-ому звену по заданному относительному положению остальных звеньев.

Рассмотрим решение обратной задачина примере плоского шарнирного четырехзвенника (рис.2.15). Введем неподвижную систему координат XY, связав ее со стойкой, и подвижные системы координат ξ¹η¹, ξ²η², ξ³η³, связав их со звеньями, как указано на рис.2.15. Условно разомкнем кинематическую цепь в точке А. При заданном значении обобщенной координаты φ₃ координаты точки А находятся из уравнений:

x_A = L₃cosφ₃ + x_O;

y_A = L₃sinφ₃ + y_O.

Для открытой кинематической цепи ABC можно записать следующие уравнения преобразования координат:

x_A = ξ_A²cosφ₂ + x_B;

y_A = ξ_A²sinφ₂ + y_B;

x_B = ξ_B¹ cosφ₁;

y_B = ξ_B¹sinφ₁.

Система состоит из 4-х уравнений с 6 неизвестными. Добавим к ней еще два очевидных уравнения:

1 = cos²φ₂ + sin²φ₂;

1 = cos²φ₁ + sin²φ₁.

Полученную систему можно привести к упрощенному виду:

x_A = L₂ a₁₁ + x_B; (2.11)

y_A = L₂ a₂₁ + y_B,

L₁ = x_B² + y_B²,

1 = a₁₁² + a₂₁²,

где a₁₁ = cosφ₁; a₂₁ = sinφ₁.

Таким образом, имеем нелинейную систему, состоящую из 4-х алгебраических уравнений относительно a₁₁, a₂₁, x_B, y_B. Одним из возможных путей решения является последовательное исключение из системы неизвестных. В результате будет получено одно уравнение с одним неизвестным:

(x_A² + y_A²) a₁₁² – 2q x_A a₁₁ + q² - y_A² = 0,

где q = (x_A²+y_A²+l₂²+l₃²) / 2l₂.

Имеем квадратное уравнение относительно a₁₁, два решения которого записываются в радикалах известным образом.

qx_A + √q2 x_A2– ( x_A2+ y_A2) (q2 – y_A2)

a₁₁= ___________________________________ ,

x_A2 + y_A2

Определив a₁₁, находим φ₂, x_B, y_B, φ₃ :

φ₂ = arccos a₁₁ ,

x_B = x_A – l₂ a₁₁ ,

y_B = y_A– l₂ a₂₁,

φ₃ = arccos (x_B / l₃) .

Для решения задачи о скоростях продифференцируем исходную систему по времени. Будем обозначать производные по времени штрихами:

(x_A)' = l₂(a₁₁)' + (x_B)' ,

(y_A)' = l₂(a₁₁)' + (y_B)' ,

0 = x_B(x_B)' + y_B(y_B)' ,

0 = a₁₁(a₁₁)' + a₂₁(a₂₁)' .

Дифференцируя эту систему еще раз по времени, получим линейную систему относительно вторых производных тех же переменных. Решение линейных систем производится одним из известных методов.

Скорости и ускорения точек и звеньев механизмов находим по формулам, записанным для краткости в матричной форме:

vy= A-1vx ;

ay= A-1ax,

(x_A)^′ (a₁₁)' (x_A)'' (a₁₁)'

(y_A)' (a₂₁)' (y_A)'' (a₂₁)'

vx= 0 , vy= (x_B)' , ax= – (x_B2 + y_B2) , ay= (x_B)'' .

0 (y_B)' – (a₁₁2 + a₂₁2) (y_B)''

Здесь A-1– обратная матрица.

1 – a₂₁x_B – a₂₁x_B a₂₁ l₂y_В

A-1=_______________ a₁₁x_B a₁₁y_B – a₁₁ – l₂x_B

l₂(a₁₁y_B– a₂₁x_B) l₂a₁₁y_B l₂a₂₁y_B – l₂a₂₁ – l₂2у_В

– l₂a₁₁x_B – l₂a₂₁x_B l₂a₁₁ l₂2x_B

Примечание. При использовании формул в матричной форме нужно знать правило умножения матрицы на вектор. Оно задаётся схемой

a₁₁ a₁₂ b₁₁ = a₁₁b₁₁+ a₁₂b₁₁

a₂₁ a₂₂ b₂₁ a₂₁b₁₁+ a₂₂b₂₁

Угловую скорость и угловое ускорение шатуна AB находим по формулам:

ω₂= –(a₁₁)' / a₂₁,

ε₂= –((a₂₁)'' + a₁₁(ω₁)'2) / a₂₁ .

Угловую скорость и угловое ускорение коромысла CB находим по формулам:

ω₃= – (x_B)' / l₃sin φ₃,

ε₃= – ((x_B)'' + l₃sin φ₃ ω₃2) / l₃sin φ₃.

Аналогичным способом получены формулы для кинематических характеристик основных рычажных механизмов, которые приводятся ниже.

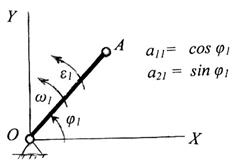
Рис.2.16. Звено, совершающее вращательное движение

Для звена, совершающего вращательное движение (кривошипа, коромысла ):

x_A= l₁a₁₁+ x₀,

y_A= l₁a₂₁+ y₀,

(x_A)' = – l₁a₁₁ω₁,

(y_A)' = l₁a₂₁ω₁,

(x_A)'' = – l₁a₁₁ω₁2– l₁a₂₁ε₁,

(y_A)'' = – l₁a₂₁ω₁2+ l₁a_11ε1.

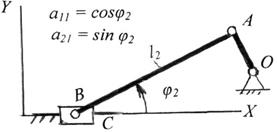
Рис. 2.17. Кривошипно-ползунный механизм

Для кривошипно-ползунного механизма:

a₂₁= y_A/ l₂,

x_A= x_B+ l₂a₁₁,

1 = a₁₁2 + a₂₁2,

Где

vy= W-1vx , ay = W-1ax ,

vx= [(x_A)', (y_A)', 0]T,

vy= [(a₁₁)', (a₂₁)', (x_B)']T,

ax = [(x_A)'', (y_A)'', –((a₁₁)'2+ (a₂₁)'2)]T,

ay = [(a₁₁)'', (a₂₁)'', x_B]T,

.

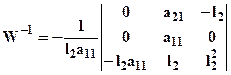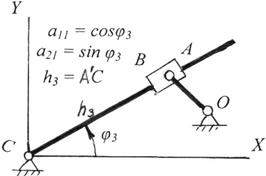
Рис.2 .18. Кулисный механизм с качающейся кулисой

Для кулисного механизма:

h₃= √ x_A2+ y_A2, x_A= h₃a₁₁, y_A= h₃a₂₁, 1 = a₁₁2 + a₂₁2,

vy= W-1vx , ay = W-1ax ,

Где

vx= [(x_A)', (y_A)', 0]T, vy= [(h₃)', (a₁₁)', (a₂₁)']T,

ax = [(x_A)'' –2(h3)'a₁₁, (y_A)'' – 2(h₃)' (a₂₁)', – ((a₁₁)'2+ (a₂₁)'2)]T,

ay = [(h3)'', (a₁₁)'', (a₂₁)'']T,

1 –h₃a₁₁ –h₃a₂₁ h₃2

W-1= – ____ –a₂₁ a₁₁a₂₁ –h₃a₁₁ .

h₃ a₁₁a₂₁ –a₁₁2 –h₃a₂₁

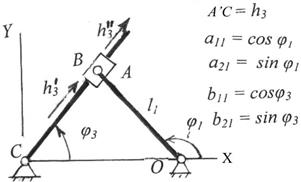
Рис. 2.19 .Кулисный механизм с ведущим камнем

Для кулисного механизма с ведущим камнем:

a₁₁= (h₃2 – x₀2 – l₁2) / (2x₀l₁) ,

(a₁₁)' = h₃(h₃)' / (x₀l₁) ,

(a₁₁)'' = ( (h₃)′ 2 + h₃(h₃)'') / (x₀l₁),

b₂₁= (x₀+ l₁a11) / h₃,

(b₂₁)' = (l₁(a₁₁)' – (h₃)' b₂₁) / h₃ ,

(b₂₁)'' = (l₁(a₁₁)'' – (h3)'' b₂₁ – 2(h₃)' b₂₁) / h₃.

2.10 . Обобщенные координаты, уравнения связей, математическая модель

пространственной кинематической цепи

Твердое тело – это система материальных точек, расстояние между которыми не изменяется при его движении.

Определим, сколько независимых координат необходимо для задания положения тела в выбранном пространстве. Каждая точка в отдельности имеет три независимые координаты. На положение точек, составляющих твердое тело, налагаются условия постоянства расстояния между ними вида r_ij = c_ij (где r_ij- расстояние между i-ой и j-ой точками, c_ijj- постоянная), из-за чего число независимых координат уменьшается. Однако для каждой точки не обязательно определять расстояние от нее до трех произвольно выбранных точек Таким образом, если задано положение трех точек твердого тела, положение остальных точек определяется с помощью приведенного выше уравнения. Три точки твердого тела также не вполне независимы. Их координаты связаны уравнениями жесткой связи r₁₂=c₁₂, r₂₃=c₂₃, r₁₃ = c₁₃, которые уменьшают число степеней свободы с девяти до шести. Итак, твердое тело обладает шестью степенями свободы : для задания его положения в пространстве требуется шесть независимых координат.

Положение твердого тела в пространстве не обязательно задавать декартовыми координатами точек. Положение произвольной точки М твердого тела в пространстве Е определяется радиус-вектором R: R = R_A + τρ ,(2.12)

где R_A – радиус-вектор начала связанной системы тела; τ – матрица направляющих косинусов связанной системы; ρ – радиус-вектор точки М в связанной системе.

Поскольку точка М – произвольная, уравнением преобразования координат (2.12) определяется положение любой точки, а значит, самого тела. В этом уравнении двенадцать переменных параметров: три декартовых координаты начала – точки А и девять направляющих косинусов τ_ij. Однако направляющие косинусы связаны шестью условиями ортогональности:

τ₁₁ ² + τ₂₁² + τ₃₁² = 1;

τ₁₂ ² + τ₂₂² + τ₃₂² = 1;

τ₁₃ ² + τ₂₃² + τ₃₃² = 1 ;(2.13)

τ₁₁τ₁₂ + τ₂₁τ₂₂ + τ₃₁τ₃₂ = 0 ;

τ₁₂τ₁₃ + τ₂₂τ₂₃ + τ₃₂τ₃₃ = 0 ;

τ₁₁τ₁₃ + τ₂₁τ₂₃ + τ₃₁τ₃₃ = 0 ,

уменьшающими число свободно задаваемых параметров тела до шести. Можно выразить матрицу τ через эйлеровы углы. Тогда независимыми координатами, определяющими положение тела, будут служить три декартовы координаты и три эйлеровых угла. Такую совокупность координат полюсов и эйлеровых углов будем называть эйлеровыми координатами тела.

Любая совокупность параметров q_s, достаточная для определения положения системы в пространстве, носит название обобщенных координат системы. Между обобщенными и декартовыми координатами точек должны существовать явные соотношения вида: x_i = x_i(q₁, q₂, …q_n).

Такими являются, в частности, соотношения (2.12).

Кинематическая цепь – это агрегат, образованный из подвижно соединенных между собой твердых тел. Из одной и той же системы тел можно получить различные агрегаты, отличающиеся друг от друга структурой (под структурой понимается способ соединения отдельных тел в агрегате). Тела соединяются с помощью устройств, называемых кинематическими парами. До объединения в связанную систему тела образовывали систему свободных тел с общим числом степеней свободы 6N, где N – число тел. При соединении тел посредством кинематических пар накладываются определенные ограничения на координаты точек этих тел, уменьшающие общее число степеней свободы системы. Соотношения, возникшие в результате соединения тел с помощью кинематических пар и связывающие обобщенные координаты, называются обобщенными уравнениями связей или просто уравнениями связей. Здесь будут рассматриваться только конечные (голономные) связи, которые накладывают ограничения на координаты точек. Они представляются в виде уравнений : F_K (q₁, q₂, …q_n) = 0 . (2.14)

Это справедливо для любой материальной системы, в том числе и для отдельного твердого тела. Так, например, в случае задания положения твердого тела с помощью направляющих косинусов, уравнениями вида (2.14) являются шесть условий ортогональности (2.13), выражающих в конечном счете неизменность расстояний между точками в твердом теле.

Обычно практический интерес представляют только пары 3—5–го классов: шаровой шарнир, шаровой шарнир с пальцем, вращательная пара (циллиндрический шарнир), поступательная пара, винтовая пара.

Очевидно, что для кинематической цепи число уравнений должно быть меньше числа переменных n (обобщенных координат), в противном случае система становится “затвердевшей”. Система уравнений (2.14) определяет mпеременных как неявные функции от остальных n-m переменных. Эти ν = n-m переменных служат независимыми обобщенными координатами кинематической цепи. Задавая их в области существования функции F_K, получим систему m уравнений с m неизвестными. Такая замкнутая система имеет определенное решение и представляет математическую модель механизма как системы, обладающей определенностью движения. В случае замкнутой цепи все уравнения (2.14) взаимосвязаны. Для открытой цепи система распадается на m независимых уравнений, что упрощает задачу.

Контрольные вопросы

1. Какие задачи решает кинематика механизмов ?

2. Что представляет собой план положений , план скоростей и план ускорений механизма?:

3. В чем преимущества и недостатки метода кинематических диаграмм ( метода графического дифференцирования) .

4. Приведите пример механизма, в котором при построениии плана ускорений учитывается ускорение Кориолиса. Приведите пример механизма, в котором при построении плана ускорений не учитывается ускорение Кориолиса. В чем здесь дело?

5. На каких уравнениях базируется аналитческий метод исследования кинематики механизмов, называемый методом преобразования координат ?

6. Как формулируется прямая задача кинематики для механизма с открытой кинематической цепью?

7. Как формулируется обратная задача кинематики механизма?

8. Почему задача о положениях шарнирного четырехзвенника имеет два решения? Какими уравнениями это подтверждается?

Почему задача о скороcтях и ускорениях имеет одно решение? Из каких уравнений это видно?

3. ДИНАМИЧЕСКИЙ АНАЛИЗ МАШИН И МЕХАНИЗМОВ

3.1. Задачи динамики машин

Динамика изучает движение с учетом действия сил инерции и инерционных свойств тел. В этом ее отличие от кинематики, которая занимается изучением собственных свойств движения и имеет только вспомогательное значение при решении динамических задач.

В динамике машин, как и в общей динамике, следует различать две задачи, прямую и обратную. Прямая задачасостоит в том, что по заданным силам находится закон движения звеньев. Обратная задача состоит в том, что по заданному закону движения находятся силы, вызвавшие это движение. В математическом отношении прямая задача сводится к интегрированию дифференциальных уравнений, обратная задача – к дифференцированию или к простому решению алгебраических уравнений.

К прямым задачам относятся рассматриваемые здесь задачи об истинном движении механизма, о регулировании хода машины, задача о маховике, к обратным задачам – силовое исследование механизма, уравновешивание роторов и механизмов. Динамические задачи можно решить лишь в том случае, если известны силы или известны движения. Поэтому в самом начале следует четко определить тип решаемой задачи.

3.2. Классификация сил в механизмах

При работе на механизм действуют силы различной природы, поэтому целесообразно произвести их классификацию.

P – движущая сила

Движущей называется сила, которая приложена к механизму со стороны двигателя и вызывает движение механизма. Движущая сила совершает положительную работу, так как ее направление всегда совпадает с направлением перемещения. Звено, к которому приложена движущая сила, называется ведущим. Движущая сила ( или момент), как правило, является функцией угловой скорости. Такая функция носит название механической характеристики двигателя. В качестве примера представлены механические характеристики двигателя внутреннего сгорания ( рис.3.1а ) и асинхронного электродвигателя (рис.3.1б).

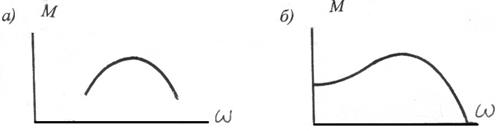
Рис. 3.1. Механические характеристики двигателей