Электротепловая аналогия
Явления теплопроводности и электропроводности описываются следующими уравнениями:
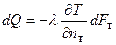
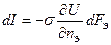 ,
,
где dQ и dI – элементарные потоки теплоты и электричества, прошедшие в единицу времени через площадки dFт, dFэ в направлении нормалей nт и nэ; U и Т – электрический потенциал и температура; l и s - коэффициенты теплопроводности и электропроводности.
В случае двумерных стационарных задач тепло- и электропроводности и независимых от температуры параметрах l и s соответствующие дифференциальное уравнения имеют вид:
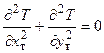 ;
;
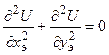 .
.
Эти уравнения имеют одинаковую структуру. Аналогичные явления должны протекать в геометрически подобных системах. Граничные условия также описываются аналогичными соотношениями.
- l gradT = aDT Þ
Þ - grad T = DT/(l/a) = DT/lт – для тепловой задачи
- grad U = DU/lэ – для электрической задачи.
Записав уравнения и граничные условия в безразмерной форме, получим тождественные уравнения.
Вывод: таким образом, видим, что распределение температуры и электрического потенциала являются подобными, то есть имеет место аналогия.
При исследовании нестационарных процессов для одномерных областей исходные дифференциальное уравнения тепло- и электропроводности имеют вид
¶Т/¶t = а∙ ¶Т2/¶хт2; (1)
¶U/¶t = (1/RэCэ )∙¶2U/¶xэ2, (2)
Скорость протекания процессов зависит от а и 1/RэCэ,
где Rэ - электрическое сопротивление на единицу длины;
Cэ - электрическая емкость на единицу длины.
Эти коэффициенты, как и коэффициент температуропроводности, не должны зависеть от температуры.
Из уравнений (1) и (2) следует, что аналогия устанавливается, если выполняется условие:
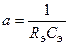
Изменение теплового потока пропорционально изменению теплоемкости системы и изменению температуры:
dQ = cт(¶T/¶tт) dtт.
Изменение электрическое тока пропорционально емкости и изменению напряжения
dI = cэ (¶U/¶tэ ) dtэ.
Следовательно, в модели теплоемкости могут быть воспроизведены соответствующими электрическими емкостями. Таким образом, можно моделировать процессы теплопроводности на электрических моделях.
При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа:
1) электрические модели повторяют геометрию оригинальной тепловой системы и изготовляются из материала с непрерывной проводимостью (электропроводящее тело или жидкий электролит) – модели с непрерывными параметрами процесса;
2) электрические модели с сосредоточенными параметрами процесса. В них тепловые системы заменяются моделирующими электрическими цепями. Также модели применяются для наиболее сложных явлений.
Для изготовления моделей с непрерывными параметрами используются тонкие листовые электропроводящие материалы. Геометрия модели в точности воспроизводит геометрию исследуемой области. Получить распределение температуры экспериментально весьма затруднительно. Поэтому исследование проводят на модели. Для измерения напряжения используется контактный зонд с нулевым прибором.
Рассмотрим электрическую модель с сосредоточенными параметрами. В этом случае исследуемая тепловая область делится на ряд элементарных объемов. Тем самым исходные дифференциальные уравнения и уравнения, описывающие условия однозначности, заменяются уравнениями в конечных разностях. Моделирующая электрическая цепь представляется в виде отдельных электрических сопротивлений, имитирующих свойства элементов тепловой области. Используются проволочные модели (из реостатного провода).
Для моделирования нестационарного теплового состояния используются RC цепи.
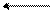


 Ra Rэ1 Rэ1 Rэ2 Rэ2
Ra Rэ1 Rэ1 Rэ2 Rэ2


















 +
+
Тв, Т1





 a; с1 с 2
a; с1 с 2



 -
-

d1 d2
Ra = 1/a;
Rэ1 = (d1/2)/l1; Rэ2 = (d2/2)/ l2.
Теплоемкости отдельных слоев воспроизводиться электрическими емкостями с1 и с2. Термические сопротивления поверхности моделируются сопротивлением Ra.
Электрическое моделирование получило широкое развитие. Применяя специальные нелинейные элементы (сопротивления) можно имитировать нелинейные граничные условия (теплообмен излучением).
Тепловая схема замещения. Тепловой закон Ома. Распределенные в пространстве теплофизические параметры заменяются сосредоточенными.
Дата добавления: 2021-09-07; просмотров: 638;











