Сравнение и аналогия

Сравнение математических фигур и величин

служит материалом для игр и обучения мудрости

Песталоцци И.Г.

В дидактике сравнение должно быть основным

приёмом

Ушинский К.Д.

Сравнение – мысленное установление сходств и различий объектов изучения. Например, сравнение параллелограмма и трапеции позволяет выделить их общие свойства: они оба четырёхугольники, оба имеют параллельные стороны, - и различие: в одном две пары параллельных сторон, в другом – одна. Сравнение обыкновенных и алгебраических дробей выявляет их сходство: наличие числителя и знаменателя, отсутствие значения, когда знаменатель обращается в нуль и различие: в одном случае числитель и знаменатель – числа, в другом алгебраические выражения.

Сравнение как метод исследования широко применяется в математике не только для изучения математических свойств объекта, но и для установления самих этих свойств. В этом смысле особую роль играет аналогия – сравнение

по сходству. Рассуждение по аналогии состоит в следующем: если два предмета или явления имеют какие–то общие признаки, то, вероятно, они могут иметь и другие общие признаки.

Схематически:

Объёкт А имеет признаки а, в, с ,х.

Объёкт В имеет признаки а, в, с.

Заключение по аналогии: вероятно объект В имеет признак х.

Заключение по аналогии следует доказать или опровергнуть.

Рассмотрим примеры рассуждений по аналогии.

По теореме Пифагора квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах. Все квадраты подобны. Построим подобные многоугольники ( на рисунке подобные треугольники) на гипотенузе и катетах так, чтобы сходственными сторонами этих многоугольников служили стороны треугольника.

Сформулируем утверждение, аналогичное теореме Пифагора: многоугольник, построенный на гипотенузе равновелик сумме подобных многоугольников, построенных на катетах. Дополнительные исследования показывают, что это верно. Распространим приведённую аналогию на кубы с ребрами, равными гипотенузе и катетам данного прямоугольного треугольника. Аналогичное утверждение о равновеликости куба, построенного на гипотенузе и суммы кубов, построенных на катетах, оказывается неверным: пусть с – гипотенуза треугольника, а и в – его катеты, тогда с>а, | a²

+с>в; | b²

ca²+c b²> a³+ b³, c(a²+ b²) > a³+ b³, c³> a³+ b³.

Аналогия имеет широкое применение в в процессе обучения математике. Приведём пример. Параллелепипед – пространственный аналог параллелограмма. В параллелограмме противоположные стороны параллельны, в параллелепипеде противоположные грани параллельны. Рассуждая по аналогии, можно прийти к гипотезе, что в параллелепипеде также как и в параллелограмме, диагонали, пересекаясь, делятся точкой пересечения пополам. Но если видеть только сходство и не замечать различия, в частности, что в параллелограмме всего две диагонали, а в параллелепипеде - четыре, то мы упустим важное свойство, подлежащее доказательству: все диагонали параллелепипеда пересекаются в одной точке.

Следовательно, применению аналогии должно предшествовать сравнение, с помощью которого выделяется как сходство, так и различие.

Используя аналогию, в школе изучают натуральные числа и десятичные дроби, обыкновенные и алгебраические дроби, сферу и окружность, круг и шар . . . Иногда аналогия оказывает «медвежью услугу» Так, по аналогии с верным свойством арифметических корней 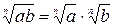учащиеся используют свойство 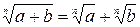, в неверности которого их можно убедить, например, для а = 9, в = 16. Такие примеры «вредных» аналогий можно продолжить. Однако полезность аналогий позволяла великому немецкому математику и астроному Иоганну Кеплеру писать: «И я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и им меньше всего следует пренебрегать в Геометрии».