Движений твердого тела
Сравнивая формулы динамики точки или поступательно движущегося тела с формулами вращательного движения тела, легко заметить, что эти формулы по структуре аналогичны. Чтобы из формул поступательного движения получить формулы вращательного движения, необходимо вместо силы подставить вращающий момент, вместо линейного перемещения — угловое перемещение, вместо линейной скорости — угловую скорость, вместо линейного ускорения — угловое ускорение, а вместо массы — момент инерции тела относительно оси вращения.
Сравнение формул поступательного и вращательного движений удобно провести с помощью табл. 17.1.
Таблица 17.1

|
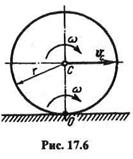
Пример 17.3.Вычислить кинетическую энергию колеса радиусом r,массой т, катящегося по прямолинейному рельсу без скольжения, если скорость центра тяжести С колеса рана 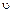 С Колесо считать сплошным однородным цилиндром (рис. 17.6).
С Колесо считать сплошным однородным цилиндром (рис. 17.6).
Решение. Решим данный пример двумя способами. Как известно из кинематики, сложное плоскопараллельное движение колеса можно рассматривать либо как простейшее вращательное движение вокруг мгновенной оси О с угловой скоростью со (метод мгновенных центров скоростей), либо как сложное движение, состоящее из поступательного движения со скоростью vc и относительного вращательного движения вокруг оси С (метод разложения плоскопараллельного движения на поступательное и вращательное). Напомним, что абсолютная (мгновенная) и относительные угловые скорости колеса всегда равны между собой.
1. Метод мгновенных центров скоростей. В этом случае кинетическая энергия колеса вычисляется по формуле
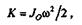
|
где Jo — момент инерции колеса относительно мгновенной оси вращения О. Момент инерции относительно оси О равен
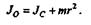
Момент инерции сплошного однородного цилиндра относительно его геометрической оси вычисляют по формуле
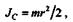
|
|
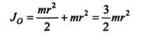
|
| следовательно, |
Теперь вычислим кинетическую энергию колеса:
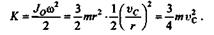
2. Метод разложения плоскопараллельного движения на поступательное и вращательное.В этом
|
случае кинетическая энергия колеса равна сумме кинетических энергий в поступательном и вращательном движениях:
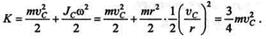
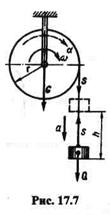
Пример 17.4. Груз Q,опускаясь, вращает однородный цилиндр, сила тяжести которого G,а радиус r (рис. 17.7). Пренебрегая трением на оси цилиндра, найти натяжение S нити, угловую скорость 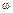 и ускорение
и ускорение  цилиндра, когда груз Q опустится на расстояние h. Вначале система находилась в покое.
цилиндра, когда груз Q опустится на расстояние h. Вначале система находилась в покое.
Решение. Для решения задачи расчленим систему на две части и рассмотрим отдельно поступательное движение груза и вращательное движение цилиндра. Так как на систему действуют постоянные силы, то груз и цилиндр будут двигаться с постоянными ускорениями а (груз) и  (цилиндр).
(цилиндр).
Линейное ускорение а груза равно касательному ускорению точек, лежащих на поверхносги цилиндра:
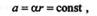
где  — угловое ускорение цилиндра.
— угловое ускорение цилиндра.
По условию начальная скорость 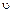 0 = 0, а конечную скорость груза, прошедшего путь h с постоянным ускорением а, определим из формулы кинематики:
0 = 0, а конечную скорость груза, прошедшего путь h с постоянным ускорением а, определим из формулы кинематики:
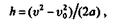
|
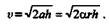
|
откуда
Далее воспользуемся теоремой об изменении кинетической энергии материальной точки и применим ее к грузу, движущемуся поступательно:
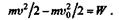
|
Подставив выражения массы, скорости и работы, получим
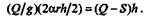
|
Отсюда реакция S нити равна
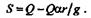
|
Далее запишем уравнение вращательного движения цилиндра
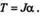
|
Вращающий момент
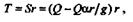
а момент инерции цилиндра вычислим по формуле
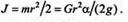
Подставив эти выражения в уравнение вращательного движения, получим
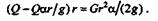
|
Отсюда определим угловое ускорение цилиндра:
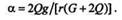
|
Теперь можно определить угловую скорость цилиндра:
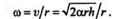
|
Подставив значение углового ускорения, получим
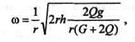
|
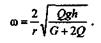
|
откуда
В заключение определим угловую скорость цилиндра с помощью теоремы об изменении кинетической энергии системы тел. Учитывая, что вначале система находилась в покое, что работа силы тяжести цилиндра равна нулю (точка ее приложения не перемещается), и пренебрегая трением, будем иметь
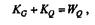
|
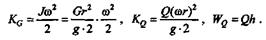
|
где
Подставив значения, получим
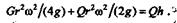
|
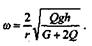
|
Отсюда
Дата добавления: 2021-09-07; просмотров: 444;











