ОСНОВЫ ДИНАМИКИ СИСТЕМЫ

МАТЕРИАЛЬНЫХ ТОЧЕК

Уравнение поступательного движения

Твердого тела

Механической системойматериальных точек называется совокупность материальных точек, каким-то образом связанных между; собой. Всякое твердое тело можно считать неизменяемой механической системой материальных точек.

Силы взаимодействия точек данной системы называются внут­ренними; силы, с которыми действуют на данную систему другие точ­ки, не входящие в эту систему, — внешними.

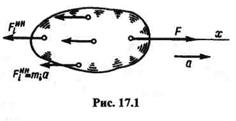
Пусть твердое тело мас­сой т движется под действием силы F поступательно с уско­рением а (рис. 17.1).

Разобьем тело на ряд ма­териальных точек с массами m_t и применим принцип Даламбера (заметим, что внутренние силы в уравнения равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю). К каждой

материальной точке приложим силу инерции 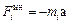и составим

уравнение равновесия:

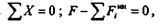
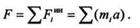
откуда

Так как при поступательном движении все точки тела имеют одина­ковые ускорения, то а можно вынести за знак суммы, т. е.

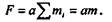
Согласно второму закону Ньютона, векторы силы Fи ускорения а совпадают по направлению, поэтому можно записать

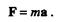
Это и есть уравнение поступательного движения твердого тела.

Это уравнение ничем не отличается от основного уравнения динами­ки точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.