Понятие о балансировке вращающихся тел
Балансировкой называется уравновешивание вращающихся или поступательно движущихся масс механизмов, с тем чтобы устранить влияние сил инерции. В настоящем параграфе рассматривается только балансировка вращающихся деталей машин.
Термины, применяемые в данном параграфе, соответствуют ГОСТ 19534—74 «Балансировка вращающихся тел. Термины».
Неуравновешенностью ротора (вращающегося в опорах тела) называется его состояние, характеризующееся таким распределени-
|
ем масс, которое за время вращения вызывает переменные нагрузки на опорах. Эти нагрузки являются причиной сотрясений и вибраций, преждевременного износа, снижают КПД и экономичность машин. Особо нежелательна неуравновешенность в быстроходных машинах.
Рассмотрим случай статической неуравновешенности, когда центр тяжести тела не лежит на оси вращения.
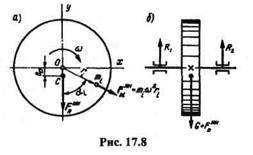
Представим себе маховик массой т,вращающийся с постоянной угловой скоростью 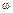 . Допустим, что центр тяжести С маховика не лежит на оси вращения, а смещен на величину ест, называемую эксцентриситетом массы (рис. 17.8).
. Допустим, что центр тяжести С маховика не лежит на оси вращения, а смещен на величину ест, называемую эксцентриситетом массы (рис. 17.8).
Силу тяжести маховика обозначим G, массой оси пренебрегаем. Разобьем маховик на ряд материальных точек с массами mi и определим равнодействующую центробежных сил инерции 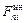 . Проекция этой равнодействующей на ось х вследствие симметрии маховика относительно оси у равна нулю, т. е.
. Проекция этой равнодействующей на ось х вследствие симметрии маховика относительно оси у равна нулю, т. е.
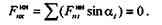
Следовательно, равнодействующая 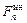 сил
сил 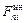 проецируется на ось у в натуральную величину. Тогда
проецируется на ось у в натуральную величину. Тогда
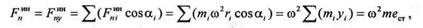
|
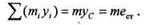
|
| так как из статики известно, что |
Таким образом, равнодействующая сил инерции всего маховика направлена по линии ОС и равна
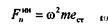
( 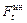 = 0, так как
= 0, так как 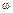 = const).
= const).
Применим принцип Даламбера и составим уравнение равновесия:
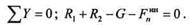
Так как сила инерции 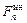 во время вращения меняет свое положение, то максимальная сила давления на подшипники будет при нижнем положении центра тяжести
во время вращения меняет свое положение, то максимальная сила давления на подшипники будет при нижнем положении центра тяжести
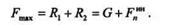
|
Определим силу давления Fmaxна подшипники, если масса маховика т = 102 кг, его частота вращения 3000 мин-1, а эксцентриситет массы ест= 1 мм.
При 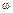 =
= 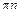 /30 =
/30 = 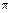 3000/30 = 100
3000/30 = 100 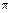 рад/с
рад/с
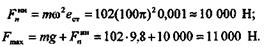
|
Как видно из примера, динамические нагрузки могут во много раз превосходить силу тяжести движущихся частей машины.
Из сказанного выше можно сделать такой вывод: для уравновешивания вращающегося тела необходимо, чтобы центр тяжести его лежал на оси вращения.
Статическую неуравновешенность легко обнаружить путем статической балансировки на двух горизонтальных параллельных балансировочных ножах. Деталь, не имеющая статической неуравновешенности, будет находиться на ножах в состоянии безразличного равновесия.
Неуравновешенность ротора характеризуется величиной дисбаланса. Произведение неуравновешенной массы на ее эксцентриситет называется значением дисбаланса и выражается в г-мм.
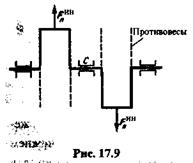
Сформулированное выше условие уравновешивания вращающегося тела не является достаточным, так как динамические нагрузки могут возникать и в том случае, когда центр тяжести лежит на оси вращения. Рассмотрим коленчатый вал двухцилиндрового двигателя (рис. 17.9).
В этом случае, даже если центр тяжести С лежит на оси вращения,
возникает пара сил инерции 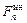 , вызывающая изгиб вала и добавочные
, вызывающая изгиб вала и добавочные
давления на опоры, меняющиеся по направлению.
|
Такая неуравновешенность называется моментной,иее можно обнаружить при достаточно быстром вращении, но не в покое. Если статическая и моментная неуравновешенности существуют одновременно, то такая неуравновешенность называется динамической. Причинами неуравновешенности могут быть неточности в изготовлении и сборке деталей, неравномерность распределения материала, деформация деталей, большие зазоры во вращательных парах и т. д.
Устраняют неуравновешенность, удаляя (например, высверливая) избыток материала в более тяжелой части детали или добавляя корректирующую массу в более легкой его части.
При значительной неуравновешенности ставят противовесы (рис. 17.9), масса которых иногда достигает десятков тысяч килограммов.
В машиностроении статическая и динамическая балансировка произ-водитсяна балансировочных станках.
Дата добавления: 2021-09-07; просмотров: 494;











