На поступательное и вращательное

В основе этого метода лежит следующая теорема: всякое плоскопа­раллельное перемещение твердого тела может быть получено с помо­щью одного поступательного и одного вращательного движения.

Пусть за время t отрезок АВ,определяющлй плоскопараллельное движение тела, переместился в положение А₁В₁ (рис. 12.9).

Предположим, что отрезок АВ вначале перемещался только поступа­тельно, причем все его точки двигались одинаково, как точка А. Таким образом, отрезок перешел в положение А₁В₂после чего его можно пере­местить в положение А₁В₁ посредством только вращательного движения вокруг точки А₁.Отсюда видно, что сложное плоскопараллельное движе­ние состоит из двух простейших движений: поступательного и враща­тельного, причем можно считать, что эти движения происходят одновре­менно.

Установим зависимость между векторами скоростей точек А и В.Для этого соединим прямыми точки А, А₁и В, В₁,В₂, в результате чего полу­чим следующую зависимость между векторами перемещений точки В:

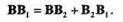
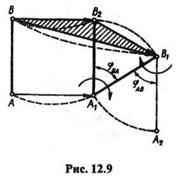
Так как ВВ₂ = АА₁, то можно записать, что

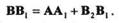
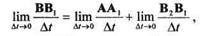
Разделим все члены равенства на t и перейдем к пределу при t, стремя­щемся к нулю:

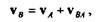
что дает

где v_B— вектор абсолютной скорости точки В; v_A — вектор абсолютной ско­рости точки А; v_ВА — вектор скорости

точки В в относительном вращательном движении отрезка АВ вокруг точ­ки А, направленный перпендикулярно отрезку АВ.

Таким образом, плоскопараллельное движение тела может осуще­ствляться путем одновременно происходящих вращательного и посту­пательного движений; поступательное движение можно считать пере­носным, а вращательное — относительным. Вектор абсолютной скоро­сти какой-то точки В равен вектору абсолютной скорости любой дру­гой точки А плюс вектор скорости точки В в относительном враща­тельном движении отрезка АВ вокруг точки А.

Точку, вокруг которой происходит относительное вращательное движение, будем называть полюсом.

Если за полюс вместо точки А принять точку В,то, рассуждая анало­гично, получим

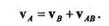
Сравнивая это векторное равенство с предыдущим, видим, что век­торы относительных скоростей v_ВА иv_АВ по модулю равны между собой, т. е.

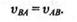
Из рис. 12.9 видно, что направление относительного вращения и угол поворота отрезка АВ за какой-то промежуток времени не зависят от вы­бора полюса, т. е.

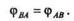
Продифференцировав это равенство по времени, получим

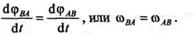
Следовательно, относительная угловая скорость от выбора полюса не зависит. Аналогично,

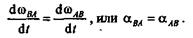
Следовательно, и относительное угловое ускорение от выбора полю­са не зависит.

Из сказанного следует, что при разложении плоскопараллельного движения на поступательное и вращательное поступательная часть движения в общем случае зависит от выбора полюса, а вращательная часть движения от выбора полюса не зависит.

Так как за полюс может быть выбрана любая точка плоскости, в том числе и мгновенный центр скоростей, то при разложении плоскопарал­лельного движения на поступательное и вращательное угловая скорость относительного вращательного движения всегда равна абсолютной угловой скорости.

Если векторное равенство v_А =v_В +v_АВ спроецировать на направле­ние прямой АВ,то

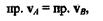
так как пр. v_АВ ⁼ 0. Следовательно, при плоскопараллельном движении проекции скоростей двух точек плоской фигуры на направление прямой, соединяющей эти точки, равны между собой.

Пример 12.2. Кривошипный механизм связан шарнирно в середине С шату­на со стержнем CD,а последний со стержнем DE, который может вращаться вокруг точки Е.Определить угловую скорость 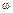_DE стержня DE в указанном на рис. 12.10 положении кривошипного механизма, если точки В и Е расположены на одной вертикали; угловая скорость ю кривошипа ОА равна 8 рад/с, ОА = 25 см, DE = 100 см, 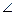CDE = 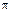/2 рад и 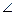BED = 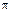/6 рад.

Решение. Прежде всего определим скорость точки А кривошипа ОА:

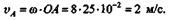
В заданном положении механизма ползун В занимает крайнее правое поло­жение и его скорость в этот момент равна нулю. Следовательно, точка В в данный момент — мгновенный центр скоростей шатуна АВ.Так как скорости точек ша­туна прямо пропорциональны их расстояниям от мгновенного центра скоростей, то запишем пропорцию

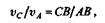
из которой определим модуль скорости точки С:

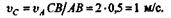
Вектор скорости v_с перпендикулярен шатуну АВ. Вектор скорости точки D перпендикулярен стержню DE, т. е. направлен вдоль стержня DC.

Скорость точки D определим, разложив сложное плоскопараллельное дви­жение звена DC на поступательное и вращательное по формуле

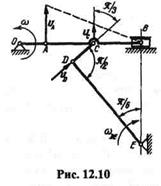
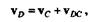
где вектор относительной скорости v_DC перпен­дикулярен звену DC. Спроецировав это векторное равенство на направление прямой DC,получим

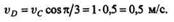
Выразив скорость точки D через угловую

скорость стержня DE,получим

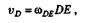
откуда, подставив числовые значения, найдем

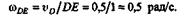
Раздел третий

ДИНАМИКА

Глава 13