Вращательное движение твердого тела.

Вращательное движение твердого тела.Вращательным называется движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.

При вращательном движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой осп.

Для определения положения вращающегося тела проведем через ось г две полуплоскости: полуплоскость I — неподвижную и полуплоскость II — связанную с твердым телом и вращающуюся вместе с ним (рис. 2.4). Тогда положение тела в любой момент времени будет однозначно определяться углом j между этими полуплоскостями, взятым с соответствующим знаком, который называется углом поворота тела.

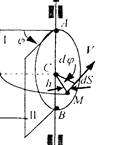
Рис. 2.4

Будем считать j > 0. если вращение наблюдается с положительного направления оси z происходящим против часовой стрелки, и j < 0. если — по часовой. Измеряется угол j в радианах.

При вращении тела угол поворота j изменяется в зависимости от времени, т. е. является функцией времени t:

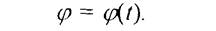(2.15)

Это уравнение называется уравнением вращательного движения твердого тела.

Основными кинематическими характеристи­ками вращательного движения твердого тела явля­ются его угловая скорость w угловое ускорение e.

Если за время Dt= t1 +tтело совершает пово­рот на Dj = j1 –j,то средняя угловая скорость тела за этот промежуток времени будет равна

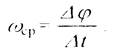(1.16)

Для определения значения угловой скорости тела в данный момент времени t найдем предел отношения приращения угла поворота Dj к промежутку времени Dtпри стремлении последнего к нулю:

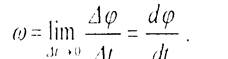(2.17)

Таким образом, угловая скорость тела в данный момент времени численно равна первой производной от угла поворота по времени. Знак угловой скорости w совпадает со знаком угла поворота тела j: w> 0 при j> 0, и наоборот, если j< 0. то и w < 0. Размерность угловой скорости обычно 1/с, так радиан величина безразмерная.

Угловую скорость можно изобразить в виде вектора w, численная величина которого равна dj/dt который направлен вдоль оси вращения тела в ту строну, откуда вращение видно происходящим против часовой стрелки.

Изменение угловой скорости тела с течением времени характеризует угловое ускорение e. По аналогии с нахождением среднего значения угловой скорости найдем выражение для определения значения среднего ускорения:

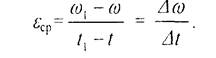(2.18)

Тогда ускорение твердого тела в данный момент времени определится из выражения

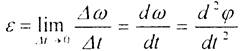(2.19)

т. е. угловое ускорение тела в данный момент времени равно первой произ­водной от угловой скорости или второй производной от угла поворота тела по времени. Размерность углового ускорения 1/с².

Угловое ускорение твердого тела так же, как и угловая скорость, может быть представлено как вектор. Вектор углового ускорения совпадает по на­правлению с вектором угловой скорости при ускоренном движении твердого юла и направлен в противоположную сторону при замедленном движении.

Установив характеристики движения твердого тела в целом, перейдем к изучению движения отдельных его точек. Рассмотрим некоторую точку М твердого тела, находящуюся на расстоянии h от оси вращения г (рис. 2.3).

При вращении тела точка М будет описывать окружное п. радиусом h с центром на оси вращения и лежащую в плоскости, перпендикулярной этой оси. Если за время dtпроисходит элементарный попорот тела па угол dj, то точка М при этом совершает вдоль своей траектории элементарное перемещение dS = h*dj,. Тогда скорость точки М определился из выражения

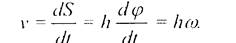(2.20)

Скорость называют линейной или окружной скоростью точки М.

Таким образом, линейная скорость точки вращающегося твердого тела численно равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Так как для всех точек тела угловая скорость w; имеет одинаковое значение, то из формулы для линейной скорости следует, что ли­нейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Линейная скорость точки твердого тела является вектором п направлена по касательной к окружности, описываемой точкой М.

Бели расстояние от оси вращения твердого пела до некоторой точки М рассматривать как радиус-вектор h точки М, то вектор линейной скорости точки v можно представить как векторное произведение вектора угловой скорости w радиус-вектор h:

V = w * h (2/21)

Действительно, результатом векторного произведения (2.21) является вектор, равный по модулю произведению w*h и направленный (рис. 2.5) перпендикулярно плоскости, в которой лежат два сомножителя, в ту сторону, откуда ближайшее совмещение первого сомножителя со вторым наблюдается происходящим против часовой стрелки, т. е. по касательной к траектории движения точки M.

Таким образом вектор, являющийся результатом векторного произведе­ния (2.21), по модулю и по направлению соответствует вектору линейной скорости точки M.

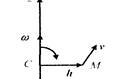
Рис. 2.5

Для нахождения выражения для ускорения а точки М выполним дифференцирование по времени выражения (2.21) для скорости точки

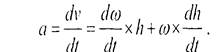(2.22)

Учитывая, что dj/dt=e, a dh/dt = v, выражение (2.22) запишем в виде

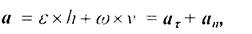(2.23)

где а_г и аnсоответственно касательная и нормальная составляющие полного ускорения точки тела при вращательном движении, определяемые из выражений

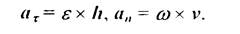(2,24)

Касательная составляющая полного ускорения точки тела (касательное ускорение) atхарактеризует изменение вектора скорости по модулю и направ­лена по касательной к траектории движения точки тела в направлении вектора скорости при ускоренном движении либо в противоположном направлении при замедленном движении. Модуль вектора касательного ускорения точки тела при вращательном движении твердого тела определяется выражением

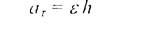(2,25)

Нормальная составляющая полного ускорения (нормальное ускорение) а„ возникает вследствие изменения направления вектора скорости точки при крашении твердого тела. Как следует из выражения (2.24) для нормального ускорения, это ускорение направлено по радиусу hк центру окружности, по которой перемещается точка. Модуль вектора нормального ускорения точки при вращательном движении твердого тела определяется с учетом (2.20) вы­ражением

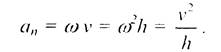(2.26)

Основные понятия сопротивления материалов

Усилия, действующие на детали механизмов, делят на внешние нагрузки и внутренние силы упругости. Внешние нагрузки, в свою очередь, разделяют на объемные и поверхностные. К объемным относятся силы веса, силы инер­ции, электромагнитные силы. Поверхностные нагрузки могут быть распреде­ленные и сосредоточенные. Сосредоточенно!! называется нагрузка, прило­женная на весьма малой по сравнению с общими размерами детали площадке. Распределенная нагрузка может быть приложена по поверхности или по ли­нии. Распределенные нагрузки измеряются в единицах интенсивности на­грузки (Н/м2, Н/м). Кроме этого, внешние нагрузки делят на заданные и реак­ции опор.

Внутренние силы упругости представляют собой силы межмолекулярно­го взаимодействия.

В результате действия внешних сил возникают упругие и пластические (остаточные) деформации. Детали машин и приборов работают, главным образом, в области упругих деформаций.

Упругостью называется свойство тела восстанавливать свои первона­чальные размеры и форму после снятия нагрузки.

Исследование деформированного состояния упругих тел производится с использованием нескольких основных гипотез:

- однородности (свойства тела в любой точке одинаковы);

- изотропности (свойства тела одинаковы во всех направлениях);

- сплошности (тело сплошным образом заполняет пространство, ограниченное его поверхностью).

Очень важным является принцип независимости действия сил и деформаций (принцип суперпозиции), который сводится к следующему: деформа­ции, возникающие в теле при действии на него данной системы уравнове­шенных сил, не зависят от деформаций, вызванных в этом же теле действием другой системы уравновешенных сил. Этот принцип справедлив при линей­ной зависимости между перемещениями точек деформированного тела и внешними силами, их вызывающими.

Метод сечений. Нормальные и касательные напряжения.Одной из основных задач расчетов на прочность является выяснение характера и величины внутренних сил упругости, действующих в нагруженной детали.

Для этого используется метол сечений, заключающийся в следующем.

Мысленно выполним сечение тела, находящегося в равновесии под действием сил F1, F2 ….Fn. плоскостью АВ (рис. 3.1).

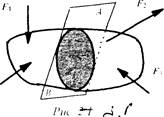
Рис. 3.1

Поскольку тело под действием указанных сил находится в равновесии, то в равновесии будет находиться и любая его часть. Отбросим мысленно правую часть и рассмотрим условие равновесия оставшейся левой части (рис. 3. 2). Для того чтобы оставшаяся часть тела находилась в равновесии, по поверхности сечения должны действовать силы, эквивалентные действию пра­вой части на левую. Такими силами яв­ляются внутренние силы упругости, рас­пределенные по сечению аб. Таким об­разом, с помощью метода сечений внут­ренние силы упругости переводятся в разряд внешних сил и для их определе­ния оказывается возможным применять соответствующие теоремы статики.

Распределенная система внутрен­них сил упругости может быть сведена к одной силе R — главному вектору внут­ренних сил упругости и к одному моменту M — главному моменту этих сил. Главный вектор R и главный момент М можно разложить на составляющие — проекции векторов на оси координат

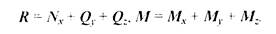(3.1)

Составляющая N_x. называемая нормальной силой, вызывает деформацию растяжения (стремится оторвать одну часть тела от другой). Составляющие Qx, Qz стремящиеся сдвинуть одну часть тела относительно другой, называют поперечными силами. Поперечные силы вызывают деформации сдвига.

Составляющая M_х главного момента вызывает деформации кручения и называется крутящим моментом. Моменты Му, и Мzизгибают тело соответствен­но в плоскостях xoz и xoy и называются изгибающими моментами. Определе­ние главного вектора R и главного момента M внутренних сил упругости (либо их составляющих) является одной из основных задач расчетов на прочность.

Интенсивность внутренних сил упругости характеризуется напряжением, которое измеряется в единицах интенсивности нагрузки, Н/м².

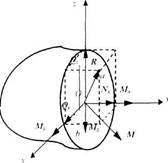
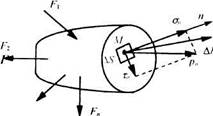
Напряжение в точке зависит от ориентации сечения, содержащего данную точку. Ориентация сечения может быть определена направлением внешней нормали к данному сечению. Рассмотрим в деформированном теле произвольное сечение с нормалью h; (рис. 3.3). Выделим около точки M данного сечения малую площадку площадью DS. Если равнодействующая сил упругости, действующих по этой площадке, будет DF, то полное напряжение pn в точке М определится как предел отношения:

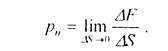(3.2)

Индекс п в обозначении напряжения свидетельствует о том, что норма­лью к рассматриваемому сечению является нормаль п. Это напряжение принято раскладывать на две составляющие - нормальную s_п и тангенциальную (касательную) tn,т. е.

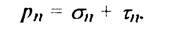(3.3)

Тогда модуль полного напряжения в точке M будет равен

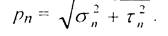(3.4)

В свою очередь вектор нормального напряжения sn можно разложить по осям координат на составляющие sxx sxy sxz. Аналогично можно получить составляющие вектора касательного напряжения tn: tnx tny tnz.

Таким образом, полное напряжение, действующее по сечению, нормаль к которому n ориентирована произвольно по отношению к координатным осям, раскладывается на шесть составляющих. Если нормалью к сечению является некоторая координатная ось, то полное напряжение раскладывается не на шесть, а только на три составляющие. Так, например, для сечения, нор­малью к которому является ось х полное напряжение р_х раскладывается на три составляющие: sxx tny tnz при этом нормальную составляющую обычно* записывают с одним индексом: sx. В соответствии с этим составляющие напряжений, действующих по сечениям, нормалями к которым являются коорди­натные оси y и z, будут обозначаться соответственно: sy tyx tyz и sz tzx tzy.