Свойства мгновенного центра скоростей

Рассматривая в каждый момент времени сложное плоскопараллель­ное движение как простейшее — вращательное, можно для вычисления скоростей точек твердого тела применять все выведенные ранее формулы вращательного движения.

Установим следующие три свойства мгновенного центра скоростей, вытекающие из закона распределения скоростей точек твердого тела, вращающегося вокруг неподвижной оси: 1) скорость мгновенного центра равна нулю; 2) мгновенный центр лежит на перпендикуляре, восставлен­ном из точки к направлению ее скорости; 3) скорость точки равна произ­ведению мгновенной угловой скорости на расстояние точки от мгновен­ного центра скоростей (рис. 12.3):

На основании перечисленных выше свойств можно установить сле­дующие пять способов определения положения мгновенного цен­тра скоростей плоской фигуры, определяющей плоскопараллельное дви­жение тела:

1. Известны мгновенная угловая скорость со и скорость 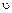_A какой-то
точки А плоской фигуры (рис. 12.3).

В этом случае мгновенный центр скоростей О находится на перпен­дикуляре, восставленном из точки А к вектору скорости 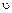_A на расстоянии OA = 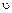_A / .

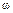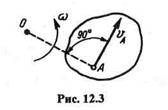
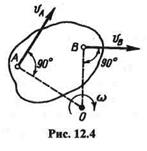
2. Известны направления скоростей двух точек А и В плоской фигу­
ры (рис. 12.4).

В этом случае мгновенный центр О лежит на пересечении перпенди­куляров, восставленных из точек А и В к направлениям их скоростей,

причем

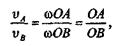
т. е. скорости точек плоской фигуры прямо пропорциональны их расстоя­ниям от мгновенного центра скоростей.

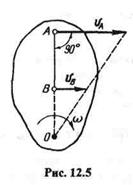
3. Известно, что скорости двух точек А и В плоской фигуры парал­
лельны друг другу, направлены в одну сторону, перпендикулярны отрезку
АВ и по модулю не равны (рис. 12.5).

В этом случае мгновенный центр скоростей О находится в точке пе­ресечения прямой, соединяющей начала векторов v_А и v_B,с прямой, со­единяющей концы этих векторов.

Если векторы скоростей точек А и В равны между собой, то мгно­венный центр скоростей в данный момент находится в бесконечности, мгновенная угловая скорость равна нулю, скорости всех точек плоской фигуры будут одинаковы и движение будет мгновенно поступательным.

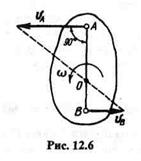
4. Известно, что скорости двух точек А и В плоской фигуры парал­
лельны друг другу, направлены в противоположные стороны и перпенди­
кулярны отрезку А В (рис. 12.6).

В этом случае мгновенный центр скоростей О находится в точке пе­ресечения отрезка АВ с прямой, соединяющей концы векторов v_А и v_B.

5. Известно, что плоская фигура катится без скольжения по непод­
вижной кривой.

В этом случае мгновенный центр скоростей О находится в точке со­прикосновения фигуры с кривой, так как скорость этой точки фигуры в данный момент равна нулю.

В заключение рассмотрим качение колеса по прямолинейному рель­су в различных условиях трения.

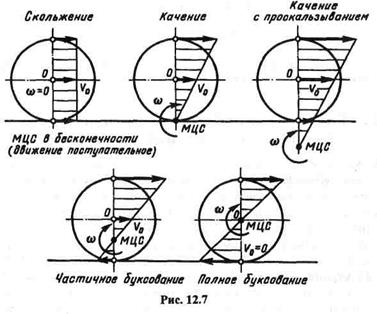
На рис. 12.7 показаны положения мгновенного центра скоростей и графики скоростей точек вертикального диаметра в случаях трения скольжения, трения качения, трения качения с проскальзыванием, час­тичного и полного буксования колеса.

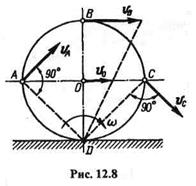
Пример 12.1.Колесо радиуса R катится без скольжения по прямолинейному рельсу, причем скорость его центра О равна v₀ = 2м/с (рис. 12.8). Найти скорость концов вертикального и горизонтального диаметров колеса.

Решение. По условию примера колесо катится без скольжения, поэтому ско­рость точки D касания колеса с рельсом равна нулю, следовательно, точка D — мгновенный центр скоростей колеса.

Зная скорость точки О, находим уг­ловую скорость со колеса:

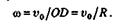
На основании свойств мгновенного центра скоростей определим модули скоростей точек А, В и С колеса:

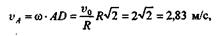
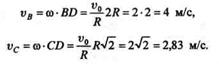
Направления векторов скоростей точек А, В и С перпендикулярны прямым, соединяющим эти точки с мгновенным центром скоростей.