Брошенной под углом к горизонту

Рассмотрим материальную точку М массой т,брошенную из точки О поверхности Земли с начальной скоростью 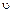₀под углом а к горизонту (рис. 13.3).

Определим движение точки М, считая, что на нее действует только сила тяжести G (сопротивлением воздуха пренебрегаем). Возьмем начало координат в точке О,ось х направим по горизонтали вправо, а ось у — по вертикали вверх. Составим дифференциальные уравнения движения точки:

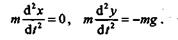
Сокращая равенства на т,получаем:

Интегрируя уравнение (13.4), находим

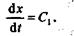
По теореме о проекции скорости на координатную ось

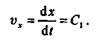
Следовательно, проекция ско­рости точки М на ось х все время остается величиной по­стоянной, равной

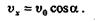
Из последних двух равенств имеем

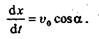
Интегрируя это уравнение, получаем

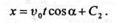
По условию при t = 0 х = 0, следовательно, произвольная постоян­ная

С₂ = 0.

Окончательно

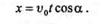
Интегрируя уравнение (13.5), находим

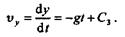
Подставив в это уравнение значение t= 0, найдем произвольную по­стоянную

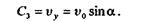
Следовательно,

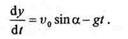
Интегрируя еще раз, получаем

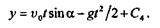
По условию при t = 0 у = 0,следовательно, произвольная постоян­ная

С₄ = 0.

Окончательно

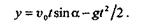
Таким образом, материальная точка М,брошенная со скоростью 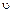₀ под углом к горизонту, движется согласно уравнениям

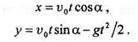
Для определения траектории точки М исключаем из полученных уравнений движения время. Определим время из первого уравнения дви­жения

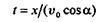
и подставим его выражение во второе уравнение, в результате чего полу­чим уравнение траектории

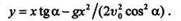
Траектория точки М представляет собой параболу с вертикальной осью симметрии.

Определим время полета точки М,для чего во второе уравнение движения подставим значение y= 0. Тогда это уравнение примет вид

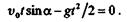
Отсюда находим два значения времени, при которых ордината равна нулю:

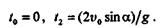
Первое значение времени соответствует началу полета, второе — его концу. Продолжительность полета

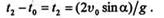
Определим дальность полета, для чего в первое уравнение движения подставим значение времени t₂:

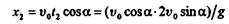
или

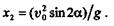
Из этого уравнения видно, что максимальная дальность полета х_mах имеет место при sin 2 = 1, т. е. при = 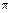/4 рад:

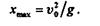
Определим наибольшую высоту подъема точки М,т. е. в тот момент, когда проекция ее скорости на ось ординат окажется равной нулю:

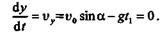
Из равенства определим t₁:

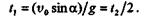
Следовательно, наибольший подъем точки имеет место в середине пути полета, т. е. при

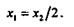
Подставив значение t₁во второе уравнение движения, получим

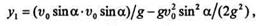
откуда

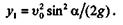
Из этого уравнения видно, что максимальной высоты точка достига­ет при sin = 1 или при = 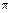/2 рад, т. е. когда точка брошена верти­кально вверх:

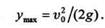
Пример 13.5. При аварии обод маховика паровой машины разорвался на не­сколько частей, которые отлетели от места аварии на разные расстояния, остава­ясь в плоскости вращения маховика. Наибольшее расстояние, на которое отлете­ли найденные куски, оказалось равным 280 м. Диаметр маховика D = 3,5 м. Опре­делить угловую скорость маховика в момент разрыва.

Решение. При рассмотрении вопроса о движении тела, брошенного под уг­лом к горизонту, была получена формула, определяющая максимальную даль­ность полета:

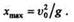
Из этой формулы определим окружную скорость маховика в момент разрыва:

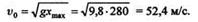
При диаметре маховика D = 3,5 м его угловая скорость в момент разрыва была равна

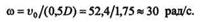
Следует заметить, что в действительности угловая скорость маховика в мо­мент разрыва была несколько больше, потому что в расчетах сопротивлением воздуха пренебрегали.

Глава 14