Формулы и графики равнопеременного
Движения точки
Как было установлено ранее, при равнопеременном движении касательное ускорение есть величина постоянная:
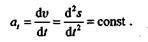
|
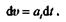
|
Отсюда
Интегрируя это выражение, получаем
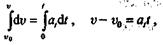
где 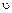 0— начальная скорость.
0— начальная скорость.
Формула скорости в окончательном виде
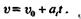
Так как
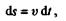
то, интегрируя это выражение, получаем формулу перемещений (расстояний от начального положения)
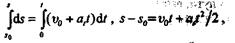
где s0 — начальное расстояние.
Полагая s0= 0, запишем формулы равнопеременного движения точки:
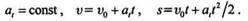
|
Если точка совершает криволинейное движение, то она имеет нормальное ускорение
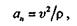
а модуль ее полного ускорения определится по формуле
|
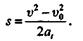
|
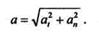
Если точка движется прямолинейно, то аn=0, а полное ускорение равно касательному: а = аt.
В равноускоренном движении направление вектора ускорения совпадает с направлением вектора скорости; в равнозамедленном движении вектор ускорения направлен в сторону, обратную вектору скорости.
Формулу перемещений (расстояний от начала отсчета) преобразуем, исключив из нее время t. Из формулы скорости имеем
тогда 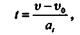
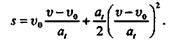
После преобразований получим
В некоторых случаях при решении задач удобно пользоваться формулой перемещений равнопеременного движения в ином виде. Так как
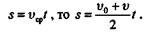
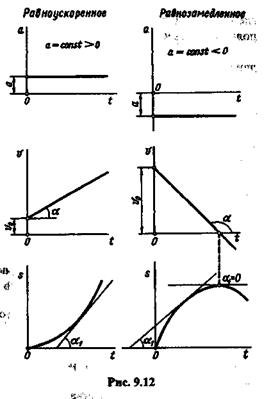
Графики ускорения, скорости и перемещения точки при прямолинейном равнопеременном движении представлены на рис. 9.12.
Кривая перемещений (расстояний) при равнопеременном движении представляет собой параболу.
Из высшей математики известно, что если построить график какой-то функции у =f(x),то в любой точке этого графика
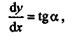
где 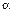 — угол, который составляет в этой точке касательная к кривой с положительным направлением оси абсцисс.
— угол, который составляет в этой точке касательная к кривой с положительным направлением оси абсцисс.
Применяя это положение к изображенным на рис. 9.12 графикам движения точки и учитывая масштабы пути и времени, получим
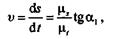
|
где 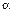 1 — угол между касательной к графику перемещения и положительным направлением оси времени;
1 — угол между касательной к графику перемещения и положительным направлением оси времени; 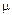 s— масштаб пути, выражаемый в м/мм;
s— масштаб пути, выражаемый в м/мм; 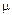 t — масштаб времени, выражаемый в с/мм.
t — масштаб времени, выражаемый в с/мм.
Из изложенного следует, что если касательная к кривой перемещений составляет острый угол с положительным направлением оси времени, то в этот момент скорость точки положительная; при тупом угле скорость точки в этот момент отрицательная. Если касательная в какой-то точке кривой перемещений параллельна оси времени, то скорость точки в этот момент равна нулю (рис. 9.12).
Аналогичная связь имеется между графиками скорости и ускорения прямолинейного движения точки, а именно
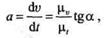
|
где 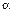 — угол между касательной к графику скорости и положительным направлением оси времени; (
— угол между касательной к графику скорости и положительным направлением оси времени; ( 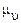 — масштаб скорости, выражаемый в (м/с)/мм.
— масштаб скорости, выражаемый в (м/с)/мм.
Нужно обратить внимание на то, что кривая перемещений при равноускоренном движении имеет выпуклость, направленную вниз (вторая производная перемещения по времени положительна), а при равнозамед-ленном движении — выпуклость, направленную вверх (вторая производная перемещения по времени отрицательна).
Пример 9.7. Вагон скатывается по наклонной плоскости с ускорением а = 0,2 м/с2. Какую скорость разовьет вагон в конце наклонной горки, длина которой 250 м? Начальная скорость вагона  0= 1 м/с.
0= 1 м/с.
Решение. Для определения скорости движения вагона в конце наклонной горки применим формулу
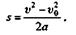
Из этой формулы найдем
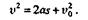
Подставляя значения величин и извлекая квадратный корень, получаем
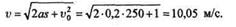
Дата добавления: 2021-09-07; просмотров: 488;











