Понятие о кривизне кривых линий
Как увидим в следующем параграфе, ускорение точки в криволинейном движении зависит от степени изогнутости ее траектории, т. е. от кривизны траектории.
Рассмотрим криволинейную траекторию точки М (рис. 9.7, а).Угол 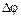 между касательными к кривой в двух соседних точках называется углом смежности.
между касательными к кривой в двух соседних точках называется углом смежности.
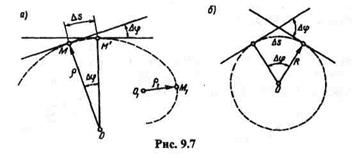
Кривизной кривой в данной точке называется предел отно-
|
шения угла смежности к соответствующей длине  s дуги, когда последняя стремится к нулю. Обозначим кривизну k,тогда
s дуги, когда последняя стремится к нулю. Обозначим кривизну k,тогда
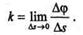
Рассмотрим окружность радиуса R (рис. 9.7, б). Так как
то
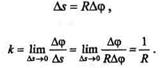
Следовательно, кривизна окружности во всех точках одинакова и равна
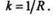
Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус 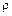 такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности называется центром кривизны.
такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности называется центром кривизны.
Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в этой же точке:
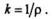
Очевидно, что кривизна прямой линии равна нулю, а радиус кривизны равен бесконечности:
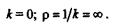
Дата добавления: 2021-09-07; просмотров: 454;











