Виды движения точки в зависимости от ускорений
Анализируя выведенные формулы касательного и нормального ускорений, можно установить следующие виды движения точки:

в этом случае движение неравномерное (  const) криволинейное (
const) криволинейное ( 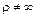 );
);

|
в этом случае движение равномерное ( 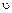 =const) криволинейное (
=const) криволинейное ( 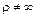 );
);
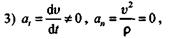
в этом случае движение неравномерное(  const) прямолинейное (
const) прямолинейное (  );
);

в этом случае движение равнопеременное (криволинейное, если ап  , прямолинейное, если ап = 0);
, прямолинейное, если ап = 0);
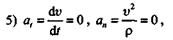
|
в этом случае движение равномерное прямолинейное, которое является единственным видом движения без ускорения.
Формулы и графики равномерного
Движения точки
Как было установлено ранее, при равномерном движении касательное ускорение аt  . Следовательно, модуль скорости точки при равномерном движении есть величина постоянная:
. Следовательно, модуль скорости точки при равномерном движении есть величина постоянная:
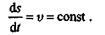
Отсюда
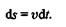

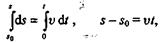
|
| Интегрируя это выражение, получаем |
где s0— начальное расстояние.
Итак, формулы равномерного движения точки имеют следующий вид:

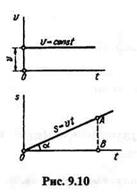
Графики скорости и пути равномерного движения показаны на рис. 9.10, причем предполагается, что s0= 0.
Нетрудно показать, что скорость точки при равномерном движении пропорциональна тангенсу угла 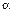 между прямолинейным графиком этого движения и положительным направлением оси времени:
между прямолинейным графиком этого движения и положительным направлением оси времени:

где 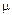 s— масштаб пути, выражаемый в м/мм;
s— масштаб пути, выражаемый в м/мм; 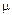 t — масштаб времени, выражаемый в с/мм.
t — масштаб времени, выражаемый в с/мм.
Пример 9.6.Первый искусственный спутник, запущенный 4 октября 1957 г. в нашей стране, имел скорость v,равную 7,78 км/с, и период обращения, равный 1 ч 30 мин, или 5400 с. Определить высоту полета спутника над поверхностью Земли, полагая его орбиту круговой, а движение равномерным. Радиус Земли принять равным R = 6370 км.
Решение. Обозначим r — радиус орбиты спутника, проведенный из центра Земли; h— искомую высоту спутника над поверхностью Земли (рис. 9.11).
Путь s,проходимый спутником за один период обращения, равен произведению времени Т,затраченного на один оборот, на скорость  движения спутника. С другой стороны, этот же путь равен длине окружности радиуса r.
движения спутника. С другой стороны, этот же путь равен длине окружности радиуса r.
Таким образом,
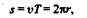
|
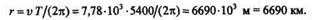
|
откуда
Далее находим искомую высоту полета:

|
Дата добавления: 2021-09-07; просмотров: 460;











