На координатную ось
|
Если движение точки задано естественным способом, то скорость ее находят как первую производную перемещения по времени; если движение точки задано в координатной форме, то с помощью теоремы о проекции скорости на координатную ось.
Теорема.Проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени.
Пусть плоское движение точки М задано координатным способом уравнениями движения
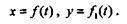
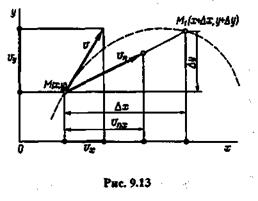
За время  t точка перешла из положения М положение М1 (рис. 9.13). Если бы точка двигалась по хорде равномерно, то ее условная скорость была бы равна
t точка перешла из положения М положение М1 (рис. 9.13). Если бы точка двигалась по хорде равномерно, то ее условная скорость была бы равна
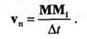
Спроецируем вектор vn и точку М на ось х,тогда
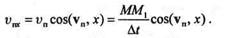
Так как
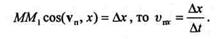
Перейдем к пределу при  t, стремящемся к нулю:
t, стремящемся к нулю:
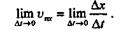
Так как скорость vn в пределе дает истинную скорость, то предел, стоящий в левой части равенства, дает проекцию истинной скорости на ось х,а правая часть есть первая производная от абсциссы х по времени, следовательно,
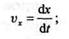
теорема доказана. Аналогично,
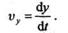
Зная две проекции скорости, можно найти ее модуль и направление по формулам:
модуль скорости
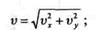
направление скорости
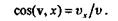
Пример 9.8.Найти модуль скорости середины М шатуна кривошипно-пол-зунного механизма и скорости ползуна В, если ОА=АВ = 0,8 м, а угол 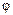 =
=  t, где
t, где 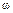 — постоянная величина, a t выражается в секундах (см. рис. 9.3)
— постоянная величина, a t выражается в секундах (см. рис. 9.3)
Решение. Для решения задачи воспользуемся уравнениями движения точки Ми ползуна В, полученными в примере 9.1:
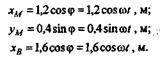
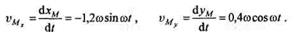
|
| Определим модуль скорости точки М: |
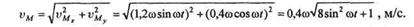
|
Для определения скорости точки М применим теорему о проекции скорости на координатную ось, в результате чего получим
Так как ползун В движется прямолинейно, то для определения модуля скорости его движения продифференцируем уравнение движения по времени, в результате чего получим
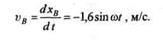
Дата добавления: 2021-09-07; просмотров: 584;











